Почему выровнять горизонт не так просто?

Выравнивание горизонта кажется одной из простейших задач при работе со снимками. Конечно, большинство фотографов хотят получить прямой горизонт, но этот участок кадра обычно обделен вниманием. А почему он не должен быть обделен? Выровнять горизонт ведь очень просто, не так ли? На практике же может потребоваться намного больше усилий, чем многие могут подумать.
Нельзя просто положиться на «виртуальный горизонт» камеры или «автовыравнивание» в ПО для постобработки, ведь человеческое восприятие уровня горизонта более сложное.
Простые случаи
Иногда не возникает совершенно никаких проблем.
В ситуациях, когда горизонт совершенно плоский и вокруг него в кадре нет очевидных отвлекающих элементов – например, морских пейзажей или широких полей – аккуратно выровнять его не составит проблем.
Конечно, уровень горизонта важен и в таких случаях. Но его намного легче достичь и при этом не требуются какие-то дополнительные шаги. Потребуется внести разве что несколько мелких коррекций направления на этапе постобработки (включая коррекцию потенциальной дисторсии).

Nikon D800E + 24мм f/1.4 @ 24мм, ISO 100, 20 с, f/11.0
Однако, такие простые примеры встречаются реже, чем вам кажется. В большинстве случаев присутствует элемент, который заставляет горизонт выглядеть неровным или искривленным. В некоторых ситуациях выраженного горизонта вообще может не быть. Тогда понадобится совершенно другой подход.
Визуальный горизонт
У каждой фотографии есть так называемый визуальный горизонт – угол, при котором фотография кажется ровной.
В кадре визуальный горизонт не всегда согласуется с действительным. Другими словами, при съемке вы можете пользоваться пузырьковым уровнем и сделать идеально ровный снимок, но все равно будет казаться будто он наклонен. Такая же ситуация происходит с «виртуальным горизонтом» камеры, использование которого может привести к получению неровных фотографий (даже если он работает идеально).
В чем причина? Если отдаленные объекты, например, длинный косогор, проходящий вдоль кадра, расположены под углом, нужно рассматривать их как новый горизонт. Если они неровные, фотография не будет выглядеть ровной, хоть каким бы идеальным ни был реальный горизонт.

Nikon D800E + 105мм f/2.8 @ 105мм, ISO 100, 1/10, f/16.0
Как видите, эта фотография выглядит достаточно ровной. Однако, на отдаленном «горизонте» виден ступенчатый косогор и мне пришлось значительно выпрямлять финальный снимок, чтобы исправить восприятие фотографии. (Другими словами, визуальный горизонт не совпадал с «технически правильным».)
Еще более сложные случаи
В ситуации с неровным холмом большинство людей согласится, что нужно наклонить рамку для получения ровной фотографии. Но зачастую попадаются значительно более сложные задачи.
Иногда определенные визуальные элементы заставляют фотографию выглядеть наклоненной даже, если это не так. Например, горизонт фотографии ниже идеально прямой, но многим покажется, что он сильно наклонен (выше в левой части и ниже в правой):

Nikon D5100 + 18-55мм f/3.5-5.6 @ 32мм, ISO 100, 6 с, f/22.0
Вот точно та же фотография, но с горизонтальной линией. Я нарисовал ее немного ниже горизонта, чтобы всё было максимально очевидно:

Горизонт абсолютно ровный.
Откуда тогда взялся наклон в исходной фотографии?
В нашем случае ответ кроется в других линиях – волнах, омывающих берег. Из-за уклона пляжа волны кажутся скошенными. Поэтому получается так, что практически все визуальные направляющие указывают на то, что справа есть сильный наклон вниз. Единственная ровная линия – сам горизонт, который недостаточно визуально выделяется, чтобы перевесить контрпримеры на переднем плане.
Это не единственный случай, когда ровный горизонт может казаться нарушителем. При правильном подходе, визуальное восприятие человека очень легко обмануть. В качестве примера, посмотрите на фигуру ниже. Ясно видно, что она наклонена (левая сторона задрана вверх, а правая опущена вниз):

На самом деле всё не так. Эта фигура абсолютно ровная. Однако, большинству людей кажется, будто она расположена под углом, поскольку на локальном уровне мозг видит, как наклонен каждый элемент, и делает вывод, что общая фигура тоже неровная. Если закрасить все линии одним цветом и добавить направляющие, становится понятно, что на самом деле квадрат не наклонен:
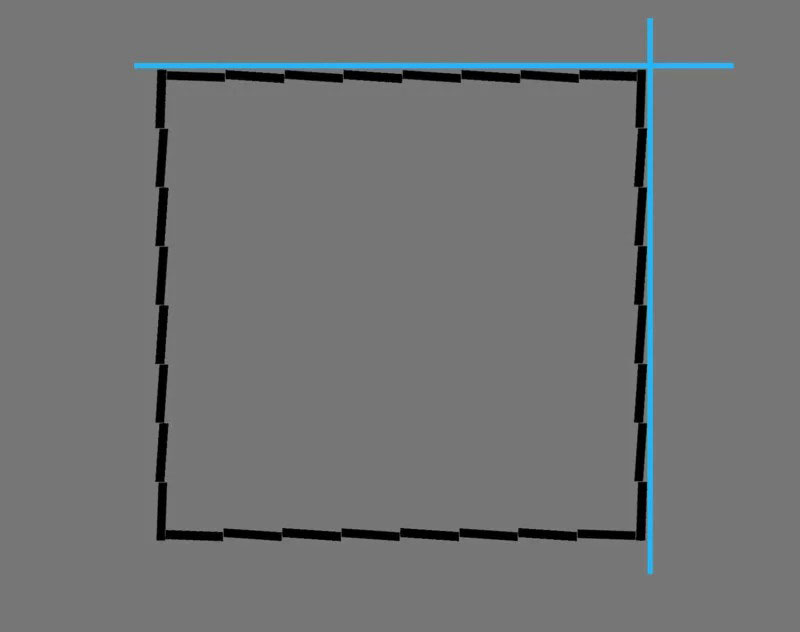
Точно такая же ситуация с фотографиями. Даже если горизонт фотографии технически правильный (при сравнении его с горизонтальной линией, нарисованной в специальном ПО), это не значит, что он выглядит плоским. Определенные визуальные элементы могут так или иначе его исказить. Снова, опирайтесь на визуальный горизонт, так как это – лучший способ придать фотографии ощущение ровности.
Что можно сделать?
Есть элементы, которые препятствуют получению фотографии с идеально ровным горизонтом:
- Неровный склон в кадре
- Заметная дисторсия объектива
- Простое отсутствие горизонта на некоторых фотографиях
- Другие обманчивые перцептивные элементы
Что делать в таких, то есть почти во всех, случаях?
Я советую работать с визуальным горизонтом. Чаще всего фотографии должны выглядеть ровным, даже если с технической точки зрения это не так.
Для этого обращайте внимание на любые визуальные подсказки в кадре. Может это дерево, которое выглядит наклоненным? Или на переднем плане есть линии, влияющие на восприятие горизонта?
Не стоит слепо доверять функции «автовыравнивания» в вашей программе для постобработки, пузырьковому уровню и встроенному виртуальному горизонту камеры. Даже ровная линия вдоль горизонта не всегда срабатывает. Хоть эти техники и работают в определенных ситуациях, они совершенно бесполезны при коррекции визуального горизонта.
Есть еще один совет, о котором я хотел бы рассказать: во время постобработки горизонтально отразите фотографию. Глядя на зеркальную версию, вы по-новому увидите снимок и заметите потенциальные проблемы с горизонтом, которые до этого были не видны.
Зеркально отразите фотографию по горизонтали.
Помимо этого, я советую время от времени пересматривать старые фотографии и обращать внимание, до сих пор ли их горизонт кажется ровным. Таким образом, вы сможете окинуть свои работы свежим взглядом, не привыкая к ним и не начиная упускать недостатки.
Выводы
Достаточно ли этих советов, чтобы все фотографии выглядели ровными? По всей вероятности, нет. Выравнивание снимков и работа с визуальным горизонтом требует времени и практики. Я могу поспорить с заявлением, что никто не может полностью овладеть этой техникой, так как каждый человек воспринимает мир по-своему. (То, что для одного выглядит совершенно прямым, другому покажется неровным.)
Тем не менее, стоит попробовать. Во многих случаях неровный горизонт создает ощущение отсутствия профессионализма или спешки. Иногда этот эффект добавляется умышленно, тем самым сводя на нет суть этой статьи! Однако, большинство фотографов все же стараются получить прямой горизонт. Если вы тоже к ним относитесь, надеюсь, что мои советы вам помогут!
Автор: Spencer Cox
Самый распространённый аргумент в пользу шарообразной Земли — это конечно же скрытие объектов за горизонтом.
И казалось бы, действительно мощное доказательство правильности официальной позиции.
— Salik.bizВ этой статье мы постараемся максимально кратко разобрать этот и ещё несколько доказательств сферичности земной поверхности.
Корабль постепенно уходит за горизонт и пропадает. Сначала низ корабля, потом середина и наконец мачта. Ура, Земля шарообразна!!!
КОРАБЛИ УХОДЯТ ЗА ГОРИЗОНТ
Посмотрим внимательно на одно из многих изображений, где корабль постепенно скрывается из виду:

На изображении мы видим как большое судно почти наполовину ушло за горизонт. Ведь мы чётко можем отследить полосу видимого горизонта.
Рекламное видео:Но когда мы спрашиваем, а почему корабль как бы находится над горизонтом и отражается в воздухе, то нам неустанно отвечают: — это всё мираж. (Фата Моргана).
Воздух как и вода имеют свойства дифракции, и поэтому изображение преломляется в лучах света, отражёнными от воды и проецируется на капельки воды содержащиеся в воздухе… (И всё в таком духе)
Такое объяснение даёт всё научное сообщество.
Но как очень часто бывает, такое объяснение нас не устраивает. — Что ещё за Фата Моргана???
Не будем ходить вокруг да около, и перейдём к сути вопроса.
На самом деле, корабль на изображении, не ушёл за горизонт. Видимая полоса горизонта, это всего лишь истинный горизонт — воображаемая полоса, где небо сливается с поверхностью Земли.
Этот термин придуман специально для шарообразной модели.
По факту же, есть просто огромная плотность воздуха, который от испарения и от нагрева приобретает практически непроницаемую полосу воздушной массы, искажённой светом (рефракцией).
Именно эта полоса не даёт увидеть объекты, которые попали в её область, и которые с удалением от наблюдателя, приобрели угловой размер меньше, чем высота рефракционной полосы (рефракционного горизонта).
Вот несколько примеров с объяснениями:

Солнце не поднялось над поверхностью воды— оно её касается.

Нет горизонта. Есть полоса рефракции, которая мешает видеть дальше.


Суша на самом деле начинается от истинного горизонта. Просто часть скрыта рефракцией.

Корабль на горизонте, но часть его скрыта полосой рефракции.
Таким образом, когда задают вопрос: — Почему мы не видим поверхность плоской Земли полностью??? Ответ таков:
Рефракционная полоса искажённого нагреванием воздуха, настолько плотная, что через неё нельзя ничего рассмотреть. Это природный «фальшивый» горизонт, за которым предметы и объекты не видны, в силу маленького углового размера.
Так как объекты с удалением становятся меньше. И когда объект удалится настолько, что его угловой размер станет меньше высоты рефракционной полосы, то разглядеть его будет невозможно.
Именно поэтому мы никогда не увидим Эйфелеву башню, статую Свободы, Родину Мать и другие высокие сооружения, если наблюдать мы их будем с такого расстояния, когда угловой размер сооружений, станет меньше высоты рефракционного горизонта.

С удалением корабля, его угловой размер станет маленьким и он скроется за рефракционной полосой.
ЗДАНИЯ НАПОЛОВИНУ СКРЫТЫЕ ЗА ГОРИЗОНТОМ
Давайте посмотрим на примеры:

Здания наполовину скрытые за горизонтом.

Ещё один пример.
Объясняется всё по тому же принципу:

Чем дальше здание, тем меньше его размер. И тем больше оно будет скрыто.

Здания находятся в пределах видимости, но из-за разных угловых размеров кажется, что они по-разному скрыты.
На изображениях показаны одни и те же здания, но с разными удалениями (угловыми размерами).
Поэтому кажется, что здания скрываются на разных высотах. И самое удалённое здание, практически не видно из-за рефракции. Хотя ровно во всех примерах, здания находятся в полной видимости.
Надо сказать, что в разное время суток и в разные времена года, полоса рефракции также изменяется. Она становится меньше, она становится более прозрачной. Поэтому вечерами и в холодное время года, наблюдения объекта становится лучше. И дальние объекты становятся виднее.
Но вернёмся к Фата Моргане.
Есть практически неоспоримый факт, что здания города Торонто, наблюдают с расстояния до 90 км.

Здания Торонто видны с большого расстояния.
Если мы обратимся к официальным данным, то получим следующее:
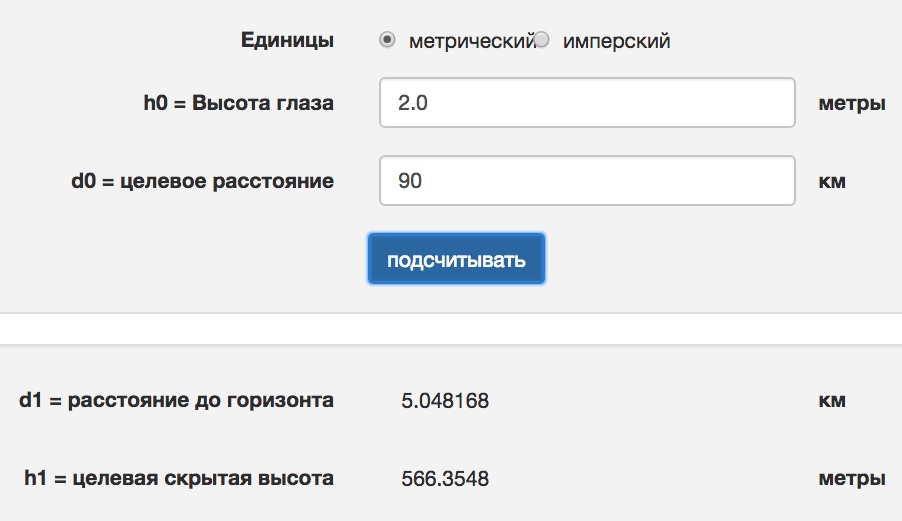
Чтобы здания были видны, они должны быть не менее километра в высоту.
Согласно геодезическому калькулятору, если наш рост около двух метров, и мы будем смотреть в оптический прибор, то максимум увидим на расстояние до 5 км.
Дальше начинается спад высоты. На удалении 90 км, спад высоты составит 560 метров.
Таким образом, если мы видим здания Торонто, на удалении 90 км, и они видны наполовину (из-за рефракционной полосы), то их высота должна составлять около 1 км в высоту. Так как 560 метров будет скрыто из-за спада высоты.
И тут учёным приходит на помощь, так называемая Фата Моргана (Мираж).
Другого объяснения найти учёные умы так и не смогли.
Однако, энтузиасты решили проверить объяснения учёных и провели эксперимент.
Суть эксперимента следующая:
На большом удалении от города Торонто, наблюдатели в оптику обнаруживают его здания. Далее они садятся в катер и плывут к Торонто, и снимают здания непрерывно, на всём пути следования.
Эксперимент показал, что здания не являются миражом, так как они были видны на всём протяжении пути.
Ролик с экспериментом:
С кораблями и зданиями разобрались, но на этом с горизонтом ещё не всё.
ГОРИЗОНТ НЕ ВСЕГДА НА УРОВНЕ ГЛАЗ
Существует выражение, что горизонт всегда на уровне глаз.
Однако приверженцы официальной версии с этим несогласны.
Их позиция строится на приборах, в которых видно, что горизонт находится ниже горизонтальной линии. Например при наборе высоты горизонт уходит вниз, и это доказательство шарообразности планеты. Поэтому утверждение якобы неверно.

Горизонт ниже линии прибора.

И здесь тоже.
Интересный аргумент. Только приборы тут не причём.
Так и должно быть. Если посмотреть на все эти изображения, то горизонт всё равно будет на уровне глаз. Это оптическая иллюзия, которая работает на любых высотах. Как бы не располагался горизонт, для нас он всегда будет на уровне глаз.
Если этого мало, то можно почитать определение из энциклопедии.
Где чёрным по белому написано, что совершенно неважно какой формы будет Земля, горизонт работает и там и там:
 Выдержка из энциклопедии.
Выдержка из энциклопедии.
Можно рассматривать массу примеров, можно рассказывать о многих аргументах, но итог всегда один:
Все доводы официальной позиции, прекрасно объясняются с позиции концепции альтернативных направлений.
© TM STUDIO
Горизонт — Википедия
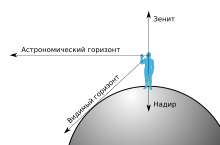 Схематичное изображение истинного (H’H), теоретического видимого (C1C2C3C4) и фактического видимого (B1B2B3B4) горизонтов.
Схематичное изображение истинного (H’H), теоретического видимого (C1C2C3C4) и фактического видимого (B1B2B3B4) горизонтов.Горизо́нт (др.-греч. ὁρίζων — буквально: ограничивающий) — граница неба с земной или водной поверхностью[1]. По другому определению в понятие включают также видимую часть этой поверхности[2]. Различают горизонт видимый и горизонт истинный. Угол между плоскостью истинного горизонта и направлением на видимый горизонт называют наклонением горизонта (синонимы: понижение горизонта, депрессия горизонта)[3]. На иллюстрации: точка A — точка наблюдения; Н’Н — плоскость истинного горизонта; отрезок AC1 — геометрическая (теоретическая) дальность видимого горизонта; дуга AB1 — географическая дальность видимого горизонта; угол α — наклонение горизонта; B1B2B3B4 — линия видимого горизонта.
Видимый горизонт
Видимым горизонтом называют и линию, по которой небо кажется граничащим с поверхностью Земли, и пространство неба над этой границей, и видимую наблюдателем поверхность Земли, и всё видимое вокруг наблюдателя пространство, до конечных пределов его[4]. Таким же образом понятие горизонта может быть определено для других небесных тел[5].
Синонимы: небосклон, кругозор, небозём, небоскат, закат неба, глазоём, зреймо, завесь, закрой, озор, овидь, окоём, оглядь[6].
Расстояние до видимого горизонта

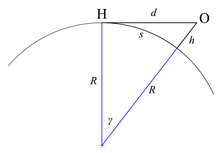 Схематический рисунок для вычисления расстояния до горизонта:
d
=
(
R
+
h
)
2
−
R
2
{\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
Схематический рисунок для вычисления расстояния до горизонта:
d
=
(
R
+
h
)
2
−
R
2
{\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}- В случае, если видимый горизонт определять как границу между небом и Землёй, то рассчитать геометрическую дальность видимого горизонта можно, воспользовавшись теоремой Пифагора:
- d = ( R + h ) 2 − R 2 {\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
- Здесь d — геометрическая дальность видимого горизонта, R — радиус Земли, h — высота точки наблюдения относительно поверхности Земли[7].
- В приближении, что Земля — идеально круглая и без учёта рефракции эта формула даёт хорошие результаты вплоть до высот расположения точки наблюдения порядка 100 км над поверхностью Земли.
- Принимая радиус Земли равным 6371 км и отбрасывая из-под корня величину h2, которая не слишком значима ввиду малого отношения h/R, получим ещё более простую приближённую формулу[8]:
- d
≈
113
h
,
{\displaystyle d\approx 113{\sqrt {h}}\,,}
где d и h в километрах или
d ≈ 3 , 57 h , {\displaystyle d\approx 3,57{\sqrt {h}}\,,}
где d в километрах, а h в метрах. - Ниже приведено расстояние до горизонта при наблюдении с различных высот[9]:
| Высота над поверхностью Земли h | Расстояние до горизонта d | Пример места наблюдения |
|---|---|---|
| 1,75 м | 4,7 км | стоя на земле |
| 25 м | 17,9 км | 8-этажный дом |
| 50 м | 25,3 км | колесо обозрения |
| 150 м | 43,8 км | воздушный шар |
| 2 км | 159,8 км | гора |
| 10 км | 357,3 км | самолёт |
| 350 км | 2114,0 км | космический корабль |
 Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.
Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.- Для облегчения расчётов дальности горизонта в зависимости от высоты точки наблюдения и с учётом рефракции составлены таблицы и номограммы. Действительные значения дальности видимого горизонта могут значительно отличаться от табличных, особенно в высоких широтах, в зависимости от состояния атмосферы и подстилающей поверхности[10][11].
- Поднятие (снижение) горизонта относится к явлениям, связанным с рефракцией (рисунок 2). При положительной рефракции видимый горизонт поднимается (расширяется), географическая дальность видимого горизонта увеличивается по сравнению с геометрической дальностью, видны предметы, обычно скрытые кривизной Земли. При нормальных температурных условиях поднятие горизонта составляет 6—7 %. При усилении температурной инверсии видимый горизонт может подняться до истинного (математического) горизонта, земная поверхность как бы распрямится, станет плоской, дальность видимости станет бесконечно большой, радиус кривизны луча станет равным радиусу земного шара. При ещё более сильной температурной инверсии видимый горизонт поднимется выше истинного. Наблюдателю будет казаться, что он находится на дне огромной котловины. Из-за горизонта поднимутся и станут видимыми (как бы парить в воздухе) предметы, находящиеся далеко за геодезическим горизонтом. При наличии сильных температурных инверсий создаются условия для возникновения верхних миражей.
- Большие градиенты температуры создаются при сильном нагреве земной поверхности солнечными лучами, часто в пустынях, в степях. Большие градиенты могут возникнуть и в средних, и даже в высоких широтах в летние дни при солнечной погоде: над песчаными пляжами, над асфальтом, над обнажённой почвой. Такие условия являются благоприятными для возникновения нижних миражей[12].
- При отрицательной рефракции видимый горизонт снижается (сужается), не видны даже те предметы, которые видны в обычных условиях.
- В случае, если видимый горизонт определять как всё видимое вокруг наблюдателя пространство, до конечных пределов его, то расстояние до видимого горизонта, например, в лесу — это максимальное расстояние на которое уходит взгляд, пока не упрётся в деревья (несколько десятков метров), а для наблюдаемой Вселенной расстояние до видимого горизонта (то есть до самых далёких звёзд, которые мы можем наблюдать) составит около 13—14 млрд световых лет[13].
- Кстати: Космический горизонт (горизонт частиц) — это и мысленно воображаемая сфера с радиусом, равным расстоянию, которое свет прошёл за время существования Вселенной, и все множество точек Вселенной, находящихся на этом расстоянии[14].
Дальность видимости
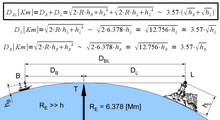 Формула и рисунок для вычисления геометрической дальности видимости.
Формула и рисунок для вычисления геометрической дальности видимости.Щёлкните по изображению, чтобы увеличить его.
На рисунке справа дальность видимости объекта определяют по формуле
D B L = 3.57 ( h B + h L ) {\displaystyle D_{\mathrm {BL} }=3.57\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})} ,
где
D
B
L
{\displaystyle D_{\mathrm {BL} }}
— дальность видимости в километрах,
h
B
{\displaystyle h_{\mathrm {B} }}
и
h
L
{\displaystyle h_{\mathrm {L} }}
— высоты точки наблюдения и объекта в метрах.
Если учесть земную рефракцию, то формула примет вид:
D B L < 3.86 ( h B + h L ) . {\displaystyle D_{\mathrm {BL} }<3.86\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
То же самое, но D B L {\displaystyle D_{\mathrm {BL} }} — в морских милях:
D B L < 2.08 ( h B + h L ) . {\displaystyle D_{\mathrm {BL} }<2.08\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
 Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).
Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).Для приближённого расчёта дальности видимости объектов применяют номограмму Струйского (см. илл.): на двух крайних шкалах номограммы отмечают точки, соответствующие высоте точки наблюдения и высоте объекта, затем проводят через них прямую и на пересечении этой прямой со средней шкалой получают дальность видимости объекта[15].
На морских картах, в лоциях и других навигационных пособиях дальность видимости маяков и огней указывается для высоты точки наблюдения равной 5 м[10]. Если высота точки наблюдения иная, то вводится поправка[16].
Горизонт на Луне
 Земля над горизонтом Луны
Земля над горизонтом ЛуныНужно сказать, что расстояния на Луне очень обманчивы. Благодаря отсутствию воздуха удалённые предметы видятся на Луне более чётко и поэтому всегда кажутся ближе.
Лунный горизонт практически вдвое ближе земного. При этом расстояние до лунного горизонта зрительно определить крайне сложно по причине отсутствия атмосферы[17], а также объектов известного размера, по которым можно бы судить о масштабе.
Истинный горизонт
Истинный горизонт — мысленно воображаемый большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии в точке наблюдения. Аналогично общему понятию, истинным горизонтом может называться не круг, а окружность, то есть линия пересечения небесной сферы и плоскости, перпендикулярной отвесной линии.
Синонимы: математический горизонт, астрономический горизонт[18].
Искусственный горизонт — прибор, которым пользуются для определения истинного горизонта.
Например, истинный горизонт легко определить, если поднести к глазам стакан с водой так, чтобы уровень воды был виден как прямая линия[19].
Горизонт в философии
Понятие горизонта в философию вводит Эдмунд Гуссерль, а Гадамер определяет его следующим образом: «Горизонт — поле зрения, охватывающее и обнимающее все то, что может быть увидено из какого-либо пункта»[20]
См. также
Примечания
- ↑ Значения слова «горизонт» на сайте gramota.ru.
- ↑ Статья «Горизонт» в Большой советской энциклопедии
- ↑ Ермолаев Г. Г., Андронов Л. П., Зотеев Е. С., Кирин Ю. П., Черниев Л. Ф. Морское судовождение / под общей редакцией капитана дальнего плавания Г. Г. Ермолаева. — издание 3-е, переработанное. — М.: Транспорт, 1970. — 568 с.
- ↑ Словари и энциклопедии на Академике. Толкования выражения «видимый горизонт». Архивировано 3 февраля 2012 года.
- ↑ Изучение Солнечной системы. Горизонт. Космос и астрономия. Архивировано 3 февраля 2012 года.
- ↑ Даль В. И. Толковый словарь живого великорусского языка. — М.: ОЛМА Медиа Групп, 2011. — 576 с. — ISBN 978-5-373-03764-8.
- ↑ Верюжский Н. А. Мореходная астрономия: Теоретический курс. — М.: РКонсульт, 2006. — 164 с. — ISBN 5-94976-802-7.
- ↑ Перельман Я. И. Горизонт // Занимательная геометрия. — М.: Римис, 2010. — 320 с. — ISBN 978-5-9650-0059-3.
- ↑ Вычислено по формуле «расстояние = 113 корней из высоты», таким образом, влияние атмосферы на распространение света не учитывается и предполагается, что Земля имеет форму шара.
- ↑ 1 2 Мореходные таблицы (МТ-2000). Адм. № 9011 / главный редактор К. А. Емец. — СПб: ГУН и О, 2002. — 576 с.
- ↑ Мир путешествий и приключений. Расчёт расстояния до горизонта и прямой видимости онлайн. Архивировано 3 февраля 2012 года.
- ↑ Всё о космосе. Какой горизонт дальше?. Архивировано 3 февраля 2012 года.
- ↑ Лукаш В. Н., Михеева Е. В. Физическая космология. — М.: Физико-математическая литература, 2010. — 404 с. — ISBN 5922111614.
- ↑ Климушкин Д. Ю.; Граблевский С. В. Космология. Космический горизонт (2001). Архивировано 3 февраля 2012 года.
- ↑ starpomlom Учебник судоводителя любителя. Глава VII . Навигация.
- ↑ Яхтенная энциклопедия. Видимый горизонт и дальность видимости. Архивировано 3 февраля 2012 года.
- ↑ Skeptic.net. Были ли американцы на Луне?. Архивировано 3 февраля 2012 года.
- ↑ Словари и энциклопедии на Академике. Толкования выражения «истинный горизонт». Архивировано 3 февраля 2012 года.
- ↑ Запаренко Виктор. Большая энциклопедия рисования Виктора Запаренко. — М.: АСТ, 2007. — 240 с. — ISBN 978-5-17-041243-3.
- ↑ Истина и метод. С.358
Литература
Горизонт — Википедия
 Схематичное изображение истинного (H’H), теоретического видимого (C1C2C3C4) и фактического видимого (B1B2B3B4) горизонтов.
Схематичное изображение истинного (H’H), теоретического видимого (C1C2C3C4) и фактического видимого (B1B2B3B4) горизонтов.Горизо́нт (др.-греч. ὁρίζων — буквально: ограничивающий) — граница неба с земной или водной поверхностью[1]. По другому определению в понятие включают также видимую часть этой поверхности[2]. Различают горизонт видимый и горизонт истинный. Угол между плоскостью истинного горизонта и направлением на видимый горизонт называют наклонением горизонта (синонимы: понижение горизонта, депрессия горизонта)[3]. На иллюстрации: точка A — точка наблюдения; Н’Н — плоскость истинного горизонта; отрезок AC1 — геометрическая (теоретическая) дальность видимого горизонта; дуга AB1 — географическая дальность видимого горизонта; угол α — наклонение горизонта; B1B2B3B4 — линия видимого горизонта.
Видимый горизонт
Видимым горизонтом называют и линию, по которой небо кажется граничащим с поверхностью Земли, и пространство неба над этой границей, и видимую наблюдателем поверхность Земли, и всё видимое вокруг наблюдателя пространство, до конечных пределов его[4]. Таким же образом понятие горизонта может быть определено для других небесных тел[5].
Синонимы: небосклон, кругозор, небозём, небоскат, закат неба, глазоём, зреймо, завесь, закрой, озор, овидь, окоём, оглядь[6].
Расстояние до видимого горизонта

 Схематический рисунок для вычисления расстояния до горизонта:
d
=
(
R
+
h
)
2
−
R
2
{\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
Схематический рисунок для вычисления расстояния до горизонта:
d
=
(
R
+
h
)
2
−
R
2
{\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}- В случае, если видимый горизонт определять как границу между небом и Землёй, то рассчитать геометрическую дальность видимого горизонта можно, воспользовавшись теоремой Пифагора:
- d = ( R + h ) 2 − R 2 {\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
- Здесь d — геометрическая дальность видимого горизонта, R — радиус Земли, h — высота точки наблюдения относительно поверхности Земли[7].
- В приближении, что Земля — идеально круглая и без учёта рефракции эта формула даёт хорошие результаты вплоть до высот расположения точки наблюдения порядка 100 км над поверхностью Земли.
- Принимая радиус Земли равным 6371 км и отбрасывая из-под корня величину h2, которая не слишком значима ввиду малого отношения h/R, получим ещё более простую приближённую формулу[8]:
- d
≈
113
h
,
{\displaystyle d\approx 113{\sqrt {h}}\,,}
где d и h в километрах или
d ≈ 3 , 57 h , {\displaystyle d\approx 3,57{\sqrt {h}}\,,}
где d в километрах, а h в метрах. - Ниже приведено расстояние до горизонта при наблюдении с различных высот[9]:
| Высота над поверхностью Земли h | Расстояние до горизонта d | Пример места наблюдения |
|---|---|---|
| 1,75 м | 4,7 км | стоя на земле |
| 25 м | 17,9 км | 8-этажный дом |
| 50 м | 25,3 км | колесо обозрения |
| 150 м | 43,8 км | воздушный шар |
| 2 км | 159,8 км | гора |
| 10 км | 357,3 км | самолёт |
| 350 км | 2114,0 км | космический корабль |
 Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.
Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.- Для облегчения расчётов дальности горизонта в зависимости от высоты точки наблюдения и с учётом рефракции составлены таблицы и номограммы. Действительные значения дальности видимого горизонта могут значительно отличаться от табличных, особенно в высоких широтах, в зависимости от состояния атмосферы и подстилающей поверхности[10][11].
- Поднятие (снижение) горизонта относится к явлениям, связанным с рефракцией (рисунок 2). При положительной рефракции видимый горизонт поднимается (расширяется), географическая дальность видимого горизонта увеличивается по сравнению с геометрической дальностью, видны предметы, обычно скрытые кривизной Земли. При нормальных температурных условиях поднятие горизонта составляет 6—7 %. При усилении температурной инверсии видимый горизонт может подняться до истинного (математического) горизонта, земная поверхность как бы распрямится, станет плоской, дальность видимости станет бесконечно большой, радиус кривизны луча станет равным радиусу земного шара. При ещё более сильной температурной инверсии видимый горизонт поднимется выше истинного. Наблюдателю будет казаться, что он находится на дне огромной котловины. Из-за горизонта поднимутся и станут видимыми (как бы парить в воздухе) предметы, находящиеся далеко за геодезическим горизонтом. При наличии сильных температурных инверсий создаются условия для возникновения верхних миражей.
- Большие градиенты температуры создаются при сильном нагреве земной поверхности солнечными лучами, часто в пустынях, в степях. Большие градиенты могут возникнуть и в средних, и даже в высоких широтах в летние дни при солнечной погоде: над песчаными пляжами, над асфальтом, над обнажённой почвой. Такие условия являются благоприятными для возникновения нижних миражей[12].
- При отрицательной рефракции видимый горизонт снижается (сужается), не видны даже те предметы, которые видны в обычных условиях.
- В случае, если видимый горизонт определять как всё видимое вокруг наблюдателя пространство, до конечных пределов его, то расстояние до видимого горизонта, например, в лесу — это максимальное расстояние на которое уходит взгляд, пока не упрётся в деревья (несколько десятков метров), а для наблюдаемой Вселенной расстояние до видимого горизонта (то есть до самых далёких звёзд, которые мы можем наблюдать) составит около 13—14 млрд световых лет[13].
- Кстати: Космический горизонт (горизонт частиц) — это и мысленно воображаемая сфера с радиусом, равным расстоянию, которое свет прошёл за время существования Вселенной, и все множество точек Вселенной, находящихся на этом расстоянии[14].
Дальность видимости
 Формула и рисунок для вычисления геометрической дальности видимости.
Формула и рисунок для вычисления геометрической дальности видимости.Щёлкните по изображению, чтобы увеличить его.
На рисунке справа дальность видимости объекта определяют по формуле
D B L = 3.57 ( h B + h L ) {\displaystyle D_{\mathrm {BL} }=3.57\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})} ,
где
D
B
L
{\displaystyle D_{\mathrm {BL} }}
— дальность видимости в километрах,
h
B
{\displaystyle h_{\mathrm {B} }}
и
h
L
{\displaystyle h_{\mathrm {L} }}
— высоты точки наблюдения и объекта в метрах.
Если учесть земную рефракцию, то формула примет вид:
D B L < 3.86 ( h B + h L ) . {\displaystyle D_{\mathrm {BL} }<3.86\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
То же самое, но D B L {\displaystyle D_{\mathrm {BL} }} — в морских милях:
D B L < 2.08 ( h B + h L ) . {\displaystyle D_{\mathrm {BL} }<2.08\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
 Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).
Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).Для приближённого расчёта дальности видимости объектов применяют номограмму Струйского (см. илл.): на двух крайних шкалах номограммы отмечают точки, соответствующие высоте точки наблюдения и высоте объекта, затем проводят через них прямую и на пересечении этой прямой со средней шкалой получают дальность видимости объекта[15].
На морских картах, в лоциях и других навигационных пособиях дальность видимости маяков и огней указывается для высоты точки наблюдения равной 5 м[10]. Если высота точки наблюдения иная, то вводится поправка[16].
Горизонт на Луне
 Земля над горизонтом Луны
Земля над горизонтом ЛуныНужно сказать, что расстояния на Луне очень обманчивы. Благодаря отсутствию воздуха удалённые предметы видятся на Луне более чётко и поэтому всегда кажутся ближе.
Лунный горизонт практически вдвое ближе земного. При этом расстояние до лунного горизонта зрительно определить крайне сложно по причине отсутствия атмосферы[17], а также объектов известного размера, по которым можно бы судить о масштабе.
Истинный горизонт
Истинный горизонт — мысленно воображаемый большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии в точке наблюдения. Аналогично общему понятию, истинным горизонтом может называться не круг, а окружность, то есть линия пересечения небесной сферы и плоскости, перпендикулярной отвесной линии.
Синонимы: математический горизонт, астрономический горизонт[18].
Искусственный горизонт — прибор, которым пользуются для определения истинного горизонта.
Например, истинный горизонт легко определить, если поднести к глазам стакан с водой так, чтобы уровень воды был виден как прямая линия[19].
Горизонт в философии
Понятие горизонта в философию вводит Эдмунд Гуссерль, а Гадамер определяет его следующим образом: «Горизонт — поле зрения, охватывающее и обнимающее все то, что может быть увидено из какого-либо пункта»[20]
См. также
Примечания
- ↑ Значения слова «горизонт» на сайте gramota.ru.
- ↑ Статья «Горизонт» в Большой советской энциклопедии
- ↑ Ермолаев Г. Г., Андронов Л. П., Зотеев Е. С., Кирин Ю. П., Черниев Л. Ф. Морское судовождение / под общей редакцией капитана дальнего плавания Г. Г. Ермолаева. — издание 3-е, переработанное. — М.: Транспорт, 1970. — 568 с.
- ↑ Словари и энциклопедии на Академике. Толкования выражения «видимый горизонт». Архивировано 3 февраля 2012 года.
- ↑ Изучение Солнечной системы. Горизонт. Космос и астрономия. Архивировано 3 февраля 2012 года.
- ↑ Даль В. И. Толковый словарь живого великорусского языка. — М.: ОЛМА Медиа Групп, 2011. — 576 с. — ISBN 978-5-373-03764-8.
- ↑ Верюжский Н. А. Мореходная астрономия: Теоретический курс. — М.: РКонсульт, 2006. — 164 с. — ISBN 5-94976-802-7.
- ↑ Перельман Я. И. Горизонт // Занимательная геометрия. — М.: Римис, 2010. — 320 с. — ISBN 978-5-9650-0059-3.
- ↑ Вычислено по формуле «расстояние = 113 корней из высоты», таким образом, влияние атмосферы на распространение света не учитывается и предполагается, что Земля имеет форму шара.
- ↑ 1 2 Мореходные таблицы (МТ-2000). Адм. № 9011 / главный редактор К. А. Емец. — СПб: ГУН и О, 2002. — 576 с.
- ↑ Мир путешествий и приключений. Расчёт расстояния до горизонта и прямой видимости онлайн. Архивировано 3 февраля 2012 года.
- ↑ Всё о космосе. Какой горизонт дальше?. Архивировано 3 февраля 2012 года.
- ↑ Лукаш В. Н., Михеева Е. В. Физическая космология. — М.: Физико-математическая литература, 2010. — 404 с. — ISBN 5922111614.
- ↑ Климушкин Д. Ю.; Граблевский С. В. Космология. Космический горизонт (2001). Архивировано 3 февраля 2012 года.
- ↑ starpomlom Учебник судоводителя любителя. Глава VII . Навигация.
- ↑ Яхтенная энциклопедия. Видимый горизонт и дальность видимости. Архивировано 3 февраля 2012 года.
- ↑ Skeptic.net. Были ли американцы на Луне?. Архивировано 3 февраля 2012 года.
- ↑ Словари и энциклопедии на Академике. Толкования выражения «истинный горизонт». Архивировано 3 февраля 2012 года.
- ↑ Запаренко Виктор. Большая энциклопедия рисования Виктора Запаренко. — М.: АСТ, 2007. — 240 с. — ISBN 978-5-17-041243-3.
- ↑ Истина и метод. С.358
Литература
Горизонт — Википедия
Схематичное изображение истинного (H’H), теоретического видимого (C1C2C3C4) и фактического видимого (B1B2B3B4) горизонтов.Горизо́нт (др.-греч. ὁρίζων — буквально: ограничивающий) — граница неба с земной или водной поверхностью[1]. По другому определению в понятие включают также видимую часть этой поверхности[2]. Различают горизонт видимый и горизонт истинный. Угол между плоскостью истинного горизонта и направлением на видимый горизонт называют наклонением горизонта (синонимы: понижение горизонта, депрессия горизонта)[3]. На иллюстрации: точка A — точка наблюдения; Н’Н — плоскость истинного горизонта; отрезок AC1 — геометрическая (теоретическая) дальность видимого горизонта; дуга AB1 — географическая дальность видимого горизонта; угол α — наклонение горизонта; B1B2B3B4 — линия видимого горизонта.
Видимый горизонт
Видимым горизонтом называют и линию, по которой небо кажется граничащим с поверхностью Земли, и пространство неба над этой границей, и видимую наблюдателем поверхность Земли, и всё видимое вокруг наблюдателя пространство, до конечных пределов его[4]. Таким же образом понятие горизонта может быть определено для других небесных тел[5].
Синонимы: небосклон, кругозор, небозём, небоскат, закат неба, глазоём, зреймо, завесь, закрой, озор, овидь, окоём, оглядь[6].
Расстояние до видимого горизонта

 Схематический рисунок для вычисления расстояния до горизонта:
d
=
(
R
+
h
)
2
−
R
2
{\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
Схематический рисунок для вычисления расстояния до горизонта:
d
=
(
R
+
h
)
2
−
R
2
{\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}- В случае, если видимый горизонт определять как границу между небом и Землёй, то рассчитать геометрическую дальность видимого горизонта можно, воспользовавшись теоремой Пифагора:
- d = ( R + h ) 2 − R 2 {\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
- Здесь d — геометрическая дальность видимого горизонта, R — радиус Земли, h — высота точки наблюдения относительно поверхности Земли[7].
- В приближении, что Земля — идеально круглая и без учёта рефракции эта формула даёт хорошие результаты вплоть до высот расположения точки наблюдения порядка 100 км над поверхностью Земли.
- Принимая радиус Земли равным 6371 км и отбрасывая из-под корня величину h2, которая не слишком значима ввиду малого отношения h/R, получим ещё более простую приближённую формулу[8]:
- d
≈
113
h
,
{\displaystyle d\approx 113{\sqrt {h}}\,,}
где d и h в километрах или
d ≈ 3 , 57 h , {\displaystyle d\approx 3,57{\sqrt {h}}\,,}
где d в километрах, а h в метрах. - Ниже приведено расстояние до горизонта при наблюдении с различных высот[9]:
| Высота над поверхностью Земли h | Расстояние до горизонта d | Пример места наблюдения |
|---|---|---|
| 1,75 м | 4,7 км | стоя на земле |
| 25 м | 17,9 км | 8-этажный дом |
| 50 м | 25,3 км | колесо обозрения |
| 150 м | 43,8 км | воздушный шар |
| 2 км | 159,8 км | гора |
| 10 км | 357,3 км | самолёт |
| 350 км | 2114,0 км | космический корабль |
 Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.
Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.- Для облегчения расчётов дальности горизонта в зависимости от высоты точки наблюдения и с учётом рефракции составлены таблицы и номограммы. Действительные значения дальности видимого горизонта могут значительно отличаться от табличных, особенно в высоких широтах, в зависимости от состояния атмосферы и подстилающей поверхности[10][11].
- Поднятие (снижение) горизонта относится к явлениям, связанным с рефракцией (рисунок 2). При положительной рефракции видимый горизонт поднимается (расширяется), географическая дальность видимого горизонта увеличивается по сравнению с геометрической дальностью, видны предметы, обычно скрытые кривизной Земли. При нормальных температурных условиях поднятие горизонта составляет 6—7 %. При усилении температурной инверсии видимый горизонт может подняться до истинного (математического) горизонта, земная поверхность как бы распрямится, станет плоской, дальность видимости станет бесконечно большой, радиус кривизны луча станет равным радиусу земного шара. При ещё более сильной температурной инверсии видимый горизонт поднимется выше истинного. Наблюдателю будет казаться, что он находится на дне огромной котловины. Из-за горизонта поднимутся и станут видимыми (как бы парить в воздухе) предметы, находящиеся далеко за геодезическим горизонтом. При наличии сильных температурных инверсий создаются условия для возникновения верхних миражей.
- Большие градиенты температуры создаются при сильном нагреве земной поверхности солнечными лучами, часто в пустынях, в степях. Большие градиенты могут возникнуть и в средних, и даже в высоких широтах в летние дни при солнечной погоде: над песчаными пляжами, над асфальтом, над обнажённой почвой. Такие условия являются благоприятными для возникновения нижних миражей[12].
- При отрицательной рефракции видимый горизонт снижается (сужается), не видны даже те предметы, которые видны в обычных условиях.
- В случае, если видимый горизонт определять как всё видимое вокруг наблюдателя пространство, до конечных пределов его, то расстояние до видимого горизонта, например, в лесу — это максимальное расстояние на которое уходит взгляд, пока не упрётся в деревья (несколько десятков метров), а для наблюдаемой Вселенной расстояние до видимого горизонта (то есть до самых далёких звёзд, которые мы можем наблюдать) составит около 13—14 млрд световых лет[13].
- Кстати: Космический горизонт (горизонт частиц) — это и мысленно воображаемая сфера с радиусом, равным расстоянию, которое свет прошёл за время существования Вселенной, и все множество точек Вселенной, находящихся на этом расстоянии[14].
Дальность видимости
 Формула и рисунок для вычисления геометрической дальности видимости.
Формула и рисунок для вычисления геометрической дальности видимости.Щёлкните по изображению, чтобы увеличить его.
На рисунке справа дальность видимости объекта определяют по формуле
D B L = 3.57 ( h B + h L ) {\displaystyle D_{\mathrm {BL} }=3.57\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})} ,
где
D
B
L
{\displaystyle D_{\mathrm {BL} }}
— дальность видимости в километрах,
h
B
{\displaystyle h_{\mathrm {B} }}
и
h
L
{\displaystyle h_{\mathrm {L} }}
— высоты точки наблюдения и объекта в метрах.
Если учесть земную рефракцию, то формула примет вид:
D B L < 3.86 ( h B + h L ) . {\displaystyle D_{\mathrm {BL} }<3.86\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
То же самое, но D B L {\displaystyle D_{\mathrm {BL} }} — в морских милях:
D B L < 2.08 ( h B + h L ) . {\displaystyle D_{\mathrm {BL} }<2.08\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
 Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).
Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).Для приближённого расчёта дальности видимости объектов применяют номограмму Струйского (см. илл.): на двух крайних шкалах номограммы отмечают точки, соответствующие высоте точки наблюдения и высоте объекта, затем проводят через них прямую и на пересечении этой прямой со средней шкалой получают дальность видимости объекта[15].
На морских картах, в лоциях и других навигационных пособиях дальность видимости маяков и огней указывается для высоты точки наблюдения равной 5 м[10]. Если высота точки наблюдения иная, то вводится поправка[16].
Горизонт на Луне
 Земля над горизонтом Луны
Земля над горизонтом ЛуныНужно сказать, что расстояния на Луне очень обманчивы. Благодаря отсутствию воздуха удалённые предметы видятся на Луне более чётко и поэтому всегда кажутся ближе.
Лунный горизонт практически вдвое ближе земного. При этом расстояние до лунного горизонта зрительно определить крайне сложно по причине отсутствия атмосферы[17], а также объектов известного размера, по которым можно бы судить о масштабе.
Истинный горизонт
Истинный горизонт — мысленно воображаемый большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии в точке наблюдения. Аналогично общему понятию, истинным горизонтом может называться не круг, а окружность, то есть линия пересечения небесной сферы и плоскости, перпендикулярной отвесной линии.
Синонимы: математический горизонт, астрономический горизонт[18].
Искусственный горизонт — прибор, которым пользуются для определения истинного горизонта.
Например, истинный горизонт легко определить, если поднести к глазам стакан с водой так, чтобы уровень воды был виден как прямая линия[19].
Горизонт в философии
Понятие горизонта в философию вводит Эдмунд Гуссерль, а Гадамер определяет его следующим образом: «Горизонт — поле зрения, охватывающее и обнимающее все то, что может быть увидено из какого-либо пункта»[20]
См. также
Примечания
- ↑ Значения слова «горизонт» на сайте gramota.ru.
- ↑ Статья «Горизонт» в Большой советской энциклопедии
- ↑ Ермолаев Г. Г., Андронов Л. П., Зотеев Е. С., Кирин Ю. П., Черниев Л. Ф. Морское судовождение / под общей редакцией капитана дальнего плавания Г. Г. Ермолаева. — издание 3-е, переработанное. — М.: Транспорт, 1970. — 568 с.
- ↑ Словари и энциклопедии на Академике. Толкования выражения «видимый горизонт». Архивировано 3 февраля 2012 года.
- ↑ Изучение Солнечной системы. Горизонт. Космос и астрономия. Архивировано 3 февраля 2012 года.
- ↑ Даль В. И. Толковый словарь живого великорусского языка. — М.: ОЛМА Медиа Групп, 2011. — 576 с. — ISBN 978-5-373-03764-8.
- ↑ Верюжский Н. А. Мореходная астрономия: Теоретический курс. — М.: РКонсульт, 2006. — 164 с. — ISBN 5-94976-802-7.
- ↑ Перельман Я. И. Горизонт // Занимательная геометрия. — М.: Римис, 2010. — 320 с. — ISBN 978-5-9650-0059-3.
- ↑ Вычислено по формуле «расстояние = 113 корней из высоты», таким образом, влияние атмосферы на распространение света не учитывается и предполагается, что Земля имеет форму шара.
- ↑ 1 2 Мореходные таблицы (МТ-2000). Адм. № 9011 / главный редактор К. А. Емец. — СПб: ГУН и О, 2002. — 576 с.
- ↑ Мир путешествий и приключений. Расчёт расстояния до горизонта и прямой видимости онлайн. Архивировано 3 февраля 2012 года.
- ↑ Всё о космосе. Какой горизонт дальше?. Архивировано 3 февраля 2012 года.
- ↑ Лукаш В. Н., Михеева Е. В. Физическая космология. — М.: Физико-математическая литература, 2010. — 404 с. — ISBN 5922111614.
- ↑ Климушкин Д. Ю.; Граблевский С. В. Космология. Космический горизонт (2001). Архивировано 3 февраля 2012 года.
- ↑ starpomlom Учебник судоводителя любителя. Глава VII . Навигация.
- ↑ Яхтенная энциклопедия. Видимый горизонт и дальность видимости. Архивировано 3 февраля 2012 года.
- ↑ Skeptic.net. Были ли американцы на Луне?. Архивировано 3 февраля 2012 года.
- ↑ Словари и энциклопедии на Академике. Толкования выражения «истинный горизонт». Архивировано 3 февраля 2012 года.
- ↑ Запаренко Виктор. Большая энциклопедия рисования Виктора Запаренко. — М.: АСТ, 2007. — 240 с. — ISBN 978-5-17-041243-3.
- ↑ Истина и метод. С.358
Литература
Горизонт — Википедия. Что такое Горизонт
 Схематичное изображение истинного (H’H), теоретического видимого (C1C2C3C4) и фактического видимого (B1B2B3B4) горизонтов.
Схематичное изображение истинного (H’H), теоретического видимого (C1C2C3C4) и фактического видимого (B1B2B3B4) горизонтов.Горизо́нт (др.-греч. ὁρίζων — буквально: ограничивающий) — граница неба с земной или водной поверхностью[1]. По другому определению в понятие включают также видимую часть этой поверхности[2]. Различают горизонт видимый и горизонт истинный. Угол между плоскостью истинного горизонта и направлением на видимый горизонт называют наклонением горизонта (синонимы: понижение горизонта, депрессия горизонта)[3]. На иллюстрации: точка A — точка наблюдения; Н’Н — плоскость истинного горизонта; отрезок AC1 — геометрическая (теоретическая) дальность видимого горизонта; дуга AB1 — географическая дальность видимого горизонта; угол α — наклонение горизонта; B1B2B3B4 — линия видимого горизонта.
Видимый горизонт
Видимым горизонтом называют и линию, по которой небо кажется граничащим с поверхностью Земли, и пространство неба над этой границей, и видимую наблюдателем поверхность Земли, и всё видимое вокруг наблюдателя пространство, до конечных пределов его[4]. Таким же образом понятие горизонта может быть определено для других небесных тел[5].
Синонимы: небосклон, кругозор, небозём, небоскат, закат неба, глазоём, зреймо, завесь, закрой, озор, овидь, окоём, оглядь[6].
Расстояние до видимого горизонта

 Схематический рисунок для вычисления расстояния до горизонта:
d
=
(
R
+
h
)
2
−
R
2
{\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
Схематический рисунок для вычисления расстояния до горизонта:
d
=
(
R
+
h
)
2
−
R
2
{\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}- В случае, если видимый горизонт определять как границу между небом и Землёй, то рассчитать геометрическую дальность видимого горизонта можно, воспользовавшись теоремой Пифагора:
- d = ( R + h ) 2 − R 2 {\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
- Здесь d — геометрическая дальность видимого горизонта, R — радиус Земли, h — высота точки наблюдения относительно поверхности Земли[7].
- В приближении, что Земля — идеально круглая и без учёта рефракции эта формула даёт хорошие результаты вплоть до высот расположения точки наблюдения порядка 100 км над поверхностью Земли.
- Принимая радиус Земли равным 6371 км и отбрасывая из-под корня величину h2, которая не слишком значима ввиду малого отношения h/R, получим ещё более простую приближённую формулу[8]:
- d
≈
113
h
,
{\displaystyle d\approx 113{\sqrt {h}}\,,}
где d и h в километрах или
d ≈ 3 , 57 h , {\displaystyle d\approx 3,57{\sqrt {h}}\,,}
где d в километрах, а h в метрах. - Ниже приведено расстояние до горизонта при наблюдении с различных высот[9]:
| Высота над поверхностью Земли h | Расстояние до горизонта d | Пример места наблюдения |
|---|---|---|
| 1,75 м | 4,7 км | стоя на земле |
| 25 м | 17,9 км | 8-этажный дом |
| 50 м | 25,3 км | колесо обозрения |
| 150 м | 43,8 км | воздушный шар |
| 2 км | 159,8 км | гора |
| 10 км | 357,3 км | самолёт |
| 350 км | 2114,0 км | космический корабль |
 Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.
Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.- Для облегчения расчётов дальности горизонта в зависимости от высоты точки наблюдения и с учётом рефракции составлены таблицы и номограммы. Действительные значения дальности видимого горизонта могут значительно отличаться от табличных, особенно в высоких широтах, в зависимости от состояния атмосферы и подстилающей поверхности[10][11].
- Поднятие (снижение) горизонта относится к явлениям, связанным с рефракцией (рисунок 2). При положительной рефракции видимый горизонт поднимается (расширяется), географическая дальность видимого горизонта увеличивается по сравнению с геометрической дальностью, видны предметы, обычно скрытые кривизной Земли. При нормальных температурных условиях поднятие горизонта составляет 6—7 %. При усилении температурной инверсии видимый горизонт может подняться до истинного (математического) горизонта, земная поверхность как бы распрямится, станет плоской, дальность видимости станет бесконечно большой, радиус кривизны луча станет равным радиусу земного шара. При ещё более сильной температурной инверсии видимый горизонт поднимется выше истинного. Наблюдателю будет казаться, что он находится на дне огромной котловины. Из-за горизонта поднимутся и станут видимыми (как бы парить в воздухе) предметы, находящиеся далеко за геодезическим горизонтом. При наличии сильных температурных инверсий создаются условия для возникновения верхних миражей.
- Большие градиенты температуры создаются при сильном нагреве земной поверхности солнечными лучами, часто в пустынях, в степях. Большие градиенты могут возникнуть и в средних, и даже в высоких широтах в летние дни при солнечной погоде: над песчаными пляжами, над асфальтом, над обнажённой почвой. Такие условия являются благоприятными для возникновения нижних миражей[12].
- При отрицательной рефракции видимый горизонт снижается (сужается), не видны даже те предметы, которые видны в обычных условиях.
- В случае, если видимый горизонт определять как всё видимое вокруг наблюдателя пространство, до конечных пределов его, то расстояние до видимого горизонта, например, в лесу — это максимальное расстояние на которое уходит взгляд, пока не упрётся в деревья (несколько десятков метров), а для наблюдаемой Вселенной расстояние до видимого горизонта (то есть до самых далёких звёзд, которые мы можем наблюдать) составит около 13—14 млрд световых лет[13].
- Кстати: Космический горизонт (горизонт частиц) — это и мысленно воображаемая сфера с радиусом, равным расстоянию, которое свет прошёл за время существования Вселенной, и все множество точек Вселенной, находящихся на этом расстоянии[14].
Дальность видимости
 Формула и рисунок для вычисления геометрической дальности видимости.
Формула и рисунок для вычисления геометрической дальности видимости.Щёлкните по изображению, чтобы увеличить его.
На рисунке справа дальность видимости объекта определяют по формуле
D B L = 3.57 ( h B + h L ) {\displaystyle D_{\mathrm {BL} }=3.57\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})} ,
где
D
B
L
{\displaystyle D_{\mathrm {BL} }}
— дальность видимости в километрах,
h
B
{\displaystyle h_{\mathrm {B} }}
и
h
L
{\displaystyle h_{\mathrm {L} }}
— высоты точки наблюдения и объекта в метрах.
Если учесть земную рефракцию, то формула примет вид:
D B L < 3.86 ( h B + h L ) . {\displaystyle D_{\mathrm {BL} }<3.86\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
То же самое, но D B L {\displaystyle D_{\mathrm {BL} }} — в морских милях:
D B L < 2.08 ( h B + h L ) . {\displaystyle D_{\mathrm {BL} }<2.08\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
 Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).
Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).Для приближённого расчёта дальности видимости объектов применяют номограмму Струйского (см. илл.): на двух крайних шкалах номограммы отмечают точки, соответствующие высоте точки наблюдения и высоте объекта, затем проводят через них прямую и на пересечении этой прямой со средней шкалой получают дальность видимости объекта[15].
На морских картах, в лоциях и других навигационных пособиях дальность видимости маяков и огней указывается для высоты точки наблюдения равной 5 м[10]. Если высота точки наблюдения иная, то вводится поправка[16].
Горизонт на Луне
 Земля над горизонтом Луны
Земля над горизонтом ЛуныНужно сказать, что расстояния на Луне очень обманчивы. Благодаря отсутствию воздуха удалённые предметы видятся на Луне более чётко и поэтому всегда кажутся ближе.
Лунный горизонт практически вдвое ближе земного. При этом расстояние до лунного горизонта зрительно определить крайне сложно по причине отсутствия атмосферы[17], а также объектов известного размера, по которым можно бы судить о масштабе.
Истинный горизонт
Истинный горизонт — мысленно воображаемый большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии в точке наблюдения. Аналогично общему понятию, истинным горизонтом может называться не круг, а окружность, то есть линия пересечения небесной сферы и плоскости, перпендикулярной отвесной линии.
Синонимы: математический горизонт, астрономический горизонт[18].
Искусственный горизонт — прибор, которым пользуются для определения истинного горизонта.
Например, истинный горизонт легко определить, если поднести к глазам стакан с водой так, чтобы уровень воды был виден как прямая линия[19].
Горизонт в философии
Понятие горизонта в философию вводит Эдмунд Гуссерль, а Гадамер определяет его следующим образом: «Горизонт — поле зрения, охватывающее и обнимающее все то, что может быть увидено из какого-либо пункта»[20]
См. также
Примечания
- ↑ Значения слова «горизонт» на сайте gramota.ru.
- ↑ Статья «Горизонт» в Большой советской энциклопедии
- ↑ Ермолаев Г. Г., Андронов Л. П., Зотеев Е. С., Кирин Ю. П., Черниев Л. Ф. Морское судовождение / под общей редакцией капитана дальнего плавания Г. Г. Ермолаева. — издание 3-е, переработанное. — М.: Транспорт, 1970. — 568 с.
- ↑ Словари и энциклопедии на Академике. Толкования выражения «видимый горизонт». Архивировано 3 февраля 2012 года.
- ↑ Изучение Солнечной системы. Горизонт. Космос и астрономия. Архивировано 3 февраля 2012 года.
- ↑ Даль В. И. Толковый словарь живого великорусского языка. — М.: ОЛМА Медиа Групп, 2011. — 576 с. — ISBN 978-5-373-03764-8.
- ↑ Верюжский Н. А. Мореходная астрономия: Теоретический курс. — М.: РКонсульт, 2006. — 164 с. — ISBN 5-94976-802-7.
- ↑ Перельман Я. И. Горизонт // Занимательная геометрия. — М.: Римис, 2010. — 320 с. — ISBN 978-5-9650-0059-3.
- ↑ Вычислено по формуле «расстояние = 113 корней из высоты», таким образом, влияние атмосферы на распространение света не учитывается и предполагается, что Земля имеет форму шара.
- ↑ 1 2 Мореходные таблицы (МТ-2000). Адм. № 9011 / главный редактор К. А. Емец. — СПб: ГУН и О, 2002. — 576 с.
- ↑ Мир путешествий и приключений. Расчёт расстояния до горизонта и прямой видимости онлайн. Архивировано 3 февраля 2012 года.
- ↑ Всё о космосе. Какой горизонт дальше?. Архивировано 3 февраля 2012 года.
- ↑ Лукаш В. Н., Михеева Е. В. Физическая космология. — М.: Физико-математическая литература, 2010. — 404 с. — ISBN 5922111614.
- ↑ Климушкин Д. Ю.; Граблевский С. В. Космология. Космический горизонт (2001). Архивировано 3 февраля 2012 года.
- ↑ starpomlom Учебник судоводителя любителя. Глава VII . Навигация.
- ↑ Яхтенная энциклопедия. Видимый горизонт и дальность видимости. Архивировано 3 февраля 2012 года.
- ↑ Skeptic.net. Были ли американцы на Луне?. Архивировано 3 февраля 2012 года.
- ↑ Словари и энциклопедии на Академике. Толкования выражения «истинный горизонт». Архивировано 3 февраля 2012 года.
- ↑ Запаренко Виктор. Большая энциклопедия рисования Виктора Запаренко. — М.: АСТ, 2007. — 240 с. — ISBN 978-5-17-041243-3.
- ↑ Истина и метод. С.358
Литература
Горизонт — Википедия Переиздание // WIKI 2

Схематичное изображение истинного (H’H), теоретического видимого (C1C2C3C4) и фактического видимого (B1B2B3B4) горизонтов.
Горизо́нт (др.-греч. ὁρίζων — буквально: ограничивающий) — граница неба с земной или водной поверхностью[1]. По другому определению в понятие включают также видимую часть этой поверхности[2]. Различают горизонт видимый и горизонт истинный. Угол между плоскостью истинного горизонта и направлением на видимый горизонт называют наклонением горизонта (синонимы: понижение горизонта, депрессия горизонта)[3]. На иллюстрации: точка A — точка наблюдения; Н’Н — плоскость истинного горизонта; отрезок AC1 — геометрическая (теоретическая) дальность видимого горизонта; дуга AB1 — географическая дальность видимого горизонта; угол α — наклонение горизонта; B1B2B3B4 — линия видимого горизонта.
Видимый горизонт
Видимым горизонтом называют и линию, по которой небо кажется граничащим с поверхностью Земли, и пространство неба над этой границей, и видимую наблюдателем поверхность Земли, и всё видимое вокруг наблюдателя пространство, до конечных пределов его[4]. Таким же образом понятие горизонта может быть определено для других небесных тел[5].
Синонимы: небосклон, кругозор, небозём, небоскат, закат неба, глазоём, зреймо, завесь, закрой, озор, овидь, окоём, оглядь[6].
Расстояние до видимого горизонта

 Схематический рисунок для вычисления расстояния до горизонта: d
= (
R
+
h ) 2 − R 2 {\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
Схематический рисунок для вычисления расстояния до горизонта: d
= (
R
+
h ) 2 − R 2 {\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}- В случае, если видимый горизонт определять как границу между небом и Землёй, то рассчитать геометрическую дальность видимого горизонта можно, воспользовавшись теоремой Пифагора:
- d = ( R + h ) 2 − R 2 {\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
- Здесь d — геометрическая дальность видимого горизонта, R — радиус Земли, h — высота точки наблюдения относительно поверхности Земли[7].
- В приближении, что Земля — идеально круглая и без учёта рефракции эта формула даёт хорошие результаты вплоть до высот расположения точки наблюдения порядка 100 км над поверхностью Земли.
- Принимая радиус Земли равным 6371 км и отбрасывая из-под корня величину h2, которая не слишком значима ввиду малого отношения h/R, получим ещё более простую приближённую формулу[8]:
- d
≈
113 h , {\displaystyle d\approx 113{\sqrt {h}}\,,}
где d и h в километрах или
d ≈ 3 , 57 h , {\displaystyle d\approx 3,57{\sqrt {h}}\,,}
где d в километрах, а h в метрах. - Ниже приведено расстояние до горизонта при наблюдении с различных высот[9]:
| Высота над поверхностью Земли h | Расстояние до горизонта d | Пример места наблюдения |
|---|---|---|
| 1,75 м | 4,7 км | стоя на земле |
| 25 м | 17,9 км | 8-этажный дом |
| 50 м | 25,3 км | колесо обозрения |
| 150 м | 43,8 км | воздушный шар |
| 2 км | 159,8 км | гора |
| 10 км | 357,3 км | самолёт |
| 350 км | 2114,0 км | космический корабль |
-

Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.
- Для облегчения расчётов дальности горизонта в зависимости от высоты точки наблюдения и с учётом рефракции составлены таблицы и номограммы. Действительные значения дальности видимого горизонта могут значительно отличаться от табличных, особенно в высоких широтах, в зависимости от состояния атмосферы и подстилающей поверхности[10][11].
- Поднятие (снижение) горизонта относится к явлениям, связанным с рефракцией (рисунок 2). При положительной рефракции видимый горизонт поднимается (расширяется), географическая дальность видимого горизонта увеличивается по сравнению с геометрической дальностью, видны предметы, обычно скрытые кривизной Земли. При нормальных температурных условиях поднятие горизонта составляет 6—7 %. При усилении температурной инверсии видимый горизонт может подняться до истинного (математического) горизонта, земная поверхность как бы распрямится, станет плоской, дальность видимости станет бесконечно большой, радиус кривизны луча станет равным радиусу земного шара. При ещё более сильной температурной инверсии видимый горизонт поднимется выше истинного. Наблюдателю будет казаться, что он находится на дне огромной котловины. Из-за горизонта поднимутся и станут видимыми (как бы парить в воздухе) предметы, находящиеся далеко за геодезическим горизонтом. При наличии сильных температурных инверсий создаются условия для возникновения верхних миражей.
- Большие градиенты температуры создаются при сильном нагреве земной поверхности солнечными лучами, часто в пустынях, в степях. Большие градиенты могут возникнуть и в средних, и даже в высоких широтах в летние дни при солнечной погоде: над песчаными пляжами, над асфальтом, над обнажённой почвой. Такие условия являются благоприятными для возникновения нижних миражей[12].
- При отрицательной рефракции видимый горизонт снижается (сужается), не видны даже те предметы, которые видны в обычных условиях.
- В случае, если видимый горизонт определять как всё видимое вокруг наблюдателя пространство, до конечных пределов его, то расстояние до видимого горизонта, например, в лесу — это максимальное расстояние на которое уходит взгляд, пока не упрётся в деревья (несколько десятков метров), а для наблюдаемой Вселенной расстояние до видимого горизонта (то есть до самых далёких звёзд, которые мы можем наблюдать) составит около 13—14 млрд световых лет[13].
- Кстати: Космический горизонт (горизонт частиц) — это и мысленно воображаемая сфера с радиусом, равным расстоянию, которое свет прошёл за время существования Вселенной, и все множество точек Вселенной, находящихся на этом расстоянии[14].
Дальность видимости

Формула и рисунок для вычисления геометрической дальности видимости.
Щёлкните по изображению, чтобы увеличить его.
На рисунке справа дальность видимости объекта определяют по формуле
D B L = 3.57 ( h B + h L ) {\displaystyle D_{\mathrm {BL} }=3.57\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})} ,
где D B
L {\displaystyle D_{\mathrm {BL} }} — дальность видимости в километрах,
h B {\displaystyle h_{\mathrm {B} }} и h L {\displaystyle h_{\mathrm {L} }} — высоты точки наблюдения и объекта в метрах.
Если учесть земную рефракцию, то формула примет вид:
D B L < 3.86 ( h B + h L ) . {\displaystyle D_{\mathrm {BL} }<3.86\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
То же самое, но D B L {\displaystyle D_{\mathrm {BL} }} — в морских милях:
D B L < 2.08 ( h B + h L ) . {\displaystyle D_{\mathrm {BL} }<2.08\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
 Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).
Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).Для приближённого расчёта дальности видимости объектов применяют номограмму Струйского (см. илл.): на двух крайних шкалах номограммы отмечают точки, соответствующие высоте точки наблюдения и высоте объекта, затем проводят через них прямую и на пересечении этой прямой со средней шкалой получают дальность видимости объекта[15].
На морских картах, в лоциях и других навигационных пособиях дальность видимости маяков и огней указывается для высоты точки наблюдения равной 5 м[10]. Если высота точки наблюдения иная, то вводится поправка[16].
Горизонт на Луне
 Земля над горизонтом Луны
Земля над горизонтом ЛуныНужно сказать, что расстояния на Луне очень обманчивы. Благодаря отсутствию воздуха удалённые предметы видятся на Луне более чётко и поэтому всегда кажутся ближе.
Лунный горизонт практически вдвое ближе земного. При этом расстояние до лунного горизонта зрительно определить крайне сложно по причине отсутствия атмосферы[17], а также объектов известного размера, по которым можно бы судить о масштабе.
Истинный горизонт
Истинный горизонт — мысленно воображаемый большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии в точке наблюдения. Аналогично общему понятию, истинным горизонтом может называться не круг, а окружность, то есть линия пересечения небесной сферы и плоскости, перпендикулярной отвесной линии.
Синонимы: математический горизонт, астрономический горизонт[18].
Искусственный горизонт — прибор, которым пользуются для определения истинного горизонта.
Например, истинный горизонт легко определить, если поднести к глазам стакан с водой так, чтобы уровень воды был виден как прямая линия[19].
Горизонт в философии
Понятие горизонта в философию вводит Эдмунд Гуссерль, а Гадамер определяет его следующим образом: «Горизонт — поле зрения, охватывающее и обнимающее все то, что может быть увидено из какого-либо пункта»[20]
См. также
Примечания
- ↑ Значения слова «горизонт» на сайте gramota.ru (неопр.).
- ↑ Статья «Горизонт» в Большой советской энциклопедии
- ↑ Ермолаев Г. Г., Андронов Л. П., Зотеев Е. С., Кирин Ю. П., Черниев Л. Ф. Морское судовождение / под общей редакцией капитана дальнего плавания Г. Г. Ермолаева. — издание 3-е, переработанное. — М.: Транспорт, 1970. — 568 с.
- ↑ [dic.academic.ru/searchall.php?SWord=%D0%B2%D0%B8%D0%B4%D0%B8%D0%BC%D1%8B%D0%B9+%D0%B3%D0%BE%D1%80%D0%B8%D0%B7%D0%BE%D0%BD%D1%82&stype=0 Словари и энциклопедии на Академике] (неопр.). Толкования выражения «видимый горизонт». Архивировано 3 февраля 2012 года.
- ↑ Изучение Солнечной системы (неопр.) (недоступная ссылка). Горизонт. Космос и астрономия. Архивировано 4 марта 2016 года.
- ↑ Даль В. И. Толковый словарь живого великорусского языка. — М.: ОЛМА Медиа Групп, 2011. — 576 с. — ISBN 978-5-373-03764-8.
- ↑ Верюжский Н. А. Мореходная астрономия: Теоретический курс. — М.: РКонсульт, 2006. — 164 с. — ISBN 5-94976-802-7.
- ↑ Перельман Я. И. Горизонт // Занимательная геометрия. — М.: Римис, 2010. — 320 с. — ISBN 978-5-9650-0059-3.
- ↑ Вычислено по формуле «расстояние = 113 корней из высоты», таким образом, влияние атмосферы на распространение света не учитывается и предполагается, что Земля имеет форму шара.
- ↑ 1 2 Мореходные таблицы (МТ-2000). Адм. № 9011 / главный редактор К. А. Емец. — СПб: ГУН и О, 2002. — 576 с.
- ↑ Мир путешествий и приключений (неопр.). Расчёт расстояния до горизонта и прямой видимости онлайн.
- ↑ Всё о космосе (неопр.) (недоступная ссылка). Какой горизонт дальше?. Архивировано 3 февраля 2012 года.
- ↑ Лукаш В. Н., Михеева Е. В. Физическая космология. — М.: Физико-математическая литература, 2010. — 404 с. — ISBN 5922111614.
- ↑ Климушкин Д. Ю.; Граблевский С. В. Космология (неопр.) (недоступная ссылка). Космический горизонт (2001). Архивировано 24 марта 2012 года.
- ↑ starpomlom Учебник судоводителя любителя (неопр.). Глава VII . Навигация.
- ↑ Яхтенная энциклопедия (неопр.) (недоступная ссылка). Видимый горизонт и дальность видимости. Архивировано 3 марта 2016 года.
- ↑ Skeptic.net (неопр.) (недоступная ссылка). Были ли американцы на Луне?. Архивировано 14 марта 2016 года.
- ↑ [dic.academic.ru/searchall.php?SWord=%D0%B8%D1%81%D1%82%D0%B8%D0%BD%D0%BD%D1%8B%D0%B9+%D0%B3%D0%BE%D1%80%D0%B8%D0%B7%D0%BE%D0%BD%D1%82&stype=0 Словари и энциклопедии на Академике] (неопр.). Толкования выражения «истинный горизонт». Архивировано 3 февраля 2012 года.
- ↑ Запаренко Виктор. Большая энциклопедия рисования Виктора Запаренко. — М.: АСТ, 2007. — 240 с. — ISBN 978-5-17-041243-3.
- ↑ Истина и метод. С.358
Литература
 Эта страница в последний раз была отредактирована 10 июня 2020 в 04:13.
Эта страница в последний раз была отредактирована 10 июня 2020 в 04:13.Почему полная луна на горизонте выглядит больше?
Время от времени в СМИ появляются изображения массивной Луны, близкой к горизонту. Увеличивается ли Луна в некоторые ночи?
Иллюзия Понзо
Оптическая иллюзия
Простой ответ на этот вопрос: нет. В то время как Луна действительно приближается к нашей планете во время ее 29,5-дневной орбиты вокруг Земли, и хотя она иногда выглядит больше, чем обычно для случайного наблюдателя на Земле, ее размер на самом деле не увеличивается.Кажущееся изменение размера нашего единственного естественного спутника, когда он находится рядом с горизонтом, является оптическим обманом. Ученые называют это Лунной иллюзией .
Supermoon — когда следующий?
Подтвердите самостоятельно
Вы можете легко подтвердить, что нет никаких изменений в размере Луны, когда она находится на горизонте, по сравнению с тем, когда она высоко в небе, выполнив очень простой эксперимент. Возьмите свою камеру и сфотографируйте Луну, когда она на горизонте. Подожди несколько часов.Теперь, используя те же настройки, сделайте еще один снимок Луны. Сравните размеры Луны на двух картинках. Вы обнаружите, что они одинаковы.
Следующая полная луна в вашем городе
Еще один способ проверить это — взять лист бумаги и свернуть его так, чтобы края рулона совпадали с краями полной луны на горизонте. Лента рулон на месте. Подождите несколько часов, а затем посмотрите на полнолуние высоко в небе через рулон. Вы обнаружите, что края рулона идеально совпадают с краями Луны.
Соблюдается с древних времен
Несмотря на то, что люди знали об иллюзии с древних времен, трудно было объяснить причину ее возникновения.
Еще в 4 веке до нашей эры греческий философ Аристотель заметил, что Луна выглядит больше, когда она находится ближе к горизонту, чем когда она находится выше в небе. Популярным объяснением оптической хитрости в то время было то, что атмосфера Земли увеличивала Луну.
Ученые теперь опровергли это объяснение — атмосфера Земли влияет на цвет Луны, но она ничего не делает для заметного изменения ее размера.
Это в наших головах
Большая полная луна в Миртл-Бич, Южная Каролина
© iStockphoto.com / LCBallard
Так что же вызывает иллюзию? Ученые не уверены. Одно популярное объяснение предполагает, что то, как мы воспринимаем размер Луны, находится в нашей голове. Другими словами, иллюзия Луны имеет психологические корни.
Люди склонны мысленно преувеличивать размер Луны относительно окружающих объектов, когда она находится на горизонте. Это потому, что, в отличие от других повседневных объектов на небе — самолетов и птиц — у людей нет контекста, чтобы определять размер небесных объектов.Согласно одному психологическому объяснению иллюзии Луны, это может заставить людей поверить, что Луна больше по сравнению с объектами на горизонте, такими как деревья и здания. Это похоже на иллюзию Ebbinghaus , которая показывает, что когда круг окружен большими кругами, он выглядит меньше, чем когда он окружен меньшими кругами.
Иллюзия неба
Другое объяснение заключается в том, как люди склонны воспринимать небо. Это объяснение, известное как теория видимого расстояния или иллюзия неба, стало популярным у арабского ученого Ибн аль-Хайтама.Он предположил, что искусственные и естественные объекты между наблюдателем и горизонтом создают иллюзию, в которой наблюдатель раздувает расстояние между ним и горизонтом по сравнению с расстоянием между ним и теми, кто находится непосредственно над ним. Это приводит к тому, что наблюдатель полагает, что горизонт Луны находится дальше и больше Луны в зените или близко к нему.
Другой версией иллюзии неба является теория плоского неба или теория видимого купола неба .Согласно этой теории, человеческий мозг воспринимает небо над нами не как купол, а как сплющенный купол, muc
.

Почему Горизонты
Когда кадр разделен одной доминирующей линией, чаще всего это происходит из-за горизонта. Они довольно распространены в уличной фотографии, особенно в пейзажах.
Если на фотографии нет ничего особенно интересного, эта линия может стать доминирующей частью фотографии, так как она разделяет рамку.
Где разместить горизонт и почему?
Во-первых, я думаю, что важно понимать, где вы не хотите размещать линию, и это находится прямо в середине кадра. Это не означает, что вы никогда не должны этого делать, это просто имеет тенденцию делить фотографию пополам, создавая неровную фотографию.
Контраст между двумя половинами делает его больше похожим на две отдельные фотографии.
Именно то, где вы располагаете горизонт, полностью зависит от вас, но это помогает помнить, что, если функция фотографии ничего не делает для ее улучшения, ей нет места на фотографии с самого начала.
Вот фотография, где горизонт разделил кадр на две части. Обратите внимание, что на самом деле это не в пользу какой-либо половины. 
Если вы возьмете горизонт и поместите его немного ниже в кадре, вы восстановите чувство стабильности, которое лучше уравновешивает фотографию.
Вы также устраняете чувство разделения, и вся фотография начинает объединяться в одно изображение, состоящее из нескольких элементов, а не просто из двух фотографий, слипшихся вместе.
Посмотрите на фото ниже, чтобы понять, что я имею в виду.
Если вы решите, что верхняя половина кадра была гораздо интереснее нижней, вы можете настроить композицию так, чтобы горизонт в кадре был намного ниже.
Фотография ниже была взята с башни в Лондоне в дождливый день с акцентом на небо.
Городской пейзаж добавляет интересную текстуру к фотографии, но при этом имеет гораздо меньший визуальный вес. Он служит для того, чтобы искусственный город выглядел маленьким по сравнению с мощным небом и погодой.
Это одно из многих интересных, дополнительных ощущений, которые можно вызвать, если учесть важность различных аспектов фотографии и соответственно скорректировать свою композицию.
Фотография ниже была сделана непосредственно после фотографии выше и сфокусирована в основном на земле, а не на небе.
Эта фотография сильно контрастирует с приведенной выше, потому что она не вызывает те же чувства, а больше фокусируется на цвете и линиях в городе.
Ваши глаза естественно нарисовали фотографию от цвета деревьев и домов внизу рамки до резкой и неровной природы зданий на небе вверху.
Не менее интересная фотография, но по разным причинам, все из-за решений, принятых по размещению горизонта.Важно отметить, что вы увидите, что оба изображения сильнее исходного изображения, которое разрезало фотографию пополам. 
Если вы хотите включить небо и землю, но не хотите разрезать фотографию пополам, я рекомендую изменить ориентацию на портретную.
Опять же, вы, вероятно, захотите избежать размещения горизонта в середине кадра, но решение остается за вами.
Я лично чувствую, что композиция на фотографии ниже сильнее любой из фотографий выше, поскольку она включает в себя самые интересные части каждой фотографии.
Погода немного изменилась между фотографиями, что означает, что на фотографии было менее неинтересное небо. Это, безусловно, помогло найти идеальный баланс между небом и землей.
Все дело в том, чтобы продумать и поэкспериментировать с тем, что работает для вас.
Хотите верьте, хотите нет, Фрэнк, они спорят об этом в течение двух тысяч лет, и пришло время исправить положение. Прежде всего, позвольте мне прояснить, что эффект является оптическим обманом. Если вы измеряете луну с помощью линейки, удерживаемой на расстоянии вытянутой руки (скрепка, согнутая в форме суппорта, также подойдет), вы обнаружите, что она всегда одинакового размера, независимо от того, где она находится в небе.Во всяком случае, Луна на меньше на на горизонте, чем в зените, главным образом потому, что она находится на расстоянии 4000 миль (радиус Земли) дальше. (Если вы не понимаете, почему это так, нарисуйте себе картину.) Тем не менее, большинство людей убеждены, что с точки зрения местности луна по меньшей мере в два раза больше, когда она близка к горизонту, чем когда она находится над головой.
Было выдвинуто множество теорий, объясняющих «лунную иллюзию». В какой-то момент люди думали, что это как-то связано с углом, под которым вы держите голову и / или глаза во время просмотра, в то время как другие говорили, что это было вызвано различиями в яркости луны при наблюдении в разных местах на небе (сначала предложено в 1709 году).Обе идеи давно уже дискредитированы. Дело в том, что иллюзия целиком зависит от визуальных сигналов, которые дает местность, когда луна приближается к горизонту, и отсутствия таких сигналов, когда она находится в зените. Чтобы доказать это, попробуйте посмотреть на луну через картонную трубку или дыру в листе бумаги, чтобы замаскировать пейзаж — иллюзия исчезнет.
То, что сейчас называется теорией «кажущейся дистанции», было впервые развито египетским астрономом Птолемеем во втором веке нашей эры (я говорил вам, что это уже давно).Его объяснение немного сбивает с толку, но здесь идет речь: большинство людей подсознательно воспринимают небо как сплющенную чашу — то есть объекты вблизи горизонта кажутся дальше, чем объекты над головой, из-за обилия визуальных сигналов на земле. Теперь, когда мы видим изображение определенного размера на большом расстоянии, мы считаем, что оно больше, чем изображение того же размера, видимое на меньшем расстоянии. (Возможно, вы захотите позволить этому фильтруться в течение минуты.) Поэтому, когда мы видим луну на «отдаленном» горизонте, мы подсознательно заключаем, что она «больше», чем когда мы видим ее через несколько часов над головой, когда она «близко» ,Другими словами, перспектива — то есть движение визуальных подсказок к горизонту — делает луну больше, чем когда она просто висит в космосе.
С этим объяснением все в порядке, но даже лучше, если мы объединим его с объяснением психолога Фрэнка Рестла. Фрэнк рассуждает так: вы судите о размере чего-либо, сравнивая его с размером вещей вокруг него. Если это окружено большими вещами, это кажется маленьким. Если он окружен мелочами, он кажется большим.Когда луна находится над головой, вы оцениваете ее размер по обширному пространству ночного неба (звезды слишком малы и слабы, чтобы что-то изменить). Ergo, это выглядит маленьким. С другой стороны, когда луна находится близко к горизонту, она обычно больше, чем многие близлежащие объекты (деревья, дома, волны в океане). Кроме того, сразу после восхода луны (когда иллюзия наиболее убедительна), видимый диаметр луны превышает расстояние от луны до горизонта. Добавьте эффект перспективы, и луна выглядит огромной.Это все, что нужно сделать.
Teeming Millions не покупают его
Уважаемый Сесил:
Я знаю, что вы не безошибочны, но на случай, если вы этого не поймете, позвольте мне указать на небольшую дезинформацию, которую вы недавно опубликовали. Вопрос был: «Почему луна иногда кажется намного больше, когда она находится рядом с горизонтом?» Или что-то в этом роде. Вы ответили, что он казался больше, потому что там были земные объекты, такие как деревья, здания и т. Д«Около» луны, давая ложную перспективу.
Извините, что разочаровал вас, но это совершенно неправильно. Атмосфера Земли, как и планета, изогнута. И, как знает любой, кто когда-либо был в бассейне, вода может искажать свет. Луна кажется больше, когда она близка к горизонту, только когда в атмосфере достаточно водяного пара (влажности), потому что кривизна земной атмосферы в сочетании с правильной плотностью пара образует то, что по сути является гигантской линзой.В этом случае увеличительная линза. Если вы докажете это, просто посмотрите на луну (или заходящее солнце) во влажный день. Любое небесное тело будет выглядеть несколько грушевидным, если находиться очень близко к горизонту, поскольку именно здесь «линза» является самой толстой. Деревья или нет деревьев.
— Том Р., Чикаго
Сесил отвечает:
Годы общения с тобой научили меня терпению, Том. Попробуйте обратить внимание. Эффект «увеличения», на который вы ссылаетесь, называется преломлением .Это объясняет тот факт, что солнце и реже луна выглядят искаженными (то есть вертикально вытянутыми или грушевидными) как раз в момент восхода или захода солнца. Удлинение длится всего несколько минут и составляет , а не , о чем говорят люди, когда говорят, что луна выглядит больше, когда она низко в небе. Так называемая иллюзия луны сохраняется, даже когда луна находится на пару градусов дуги над горизонтом.
Иллюзия полностью психологическая по происхождению. Фактический размер изображения луны не уменьшается, поскольку он поднимается в небе; Вы только думаете, что это так.Чтобы доказать это еще раз, я недавно встал в нескольких точках ночью и попробовал описанный выше тест на скрепку для скрепок, чтобы измерить размер изображения луны, когда она опускалась к горизонту. Иллюзия большого размера была непреодолимой к концу, но она исчезла, как только я поднял скрепку и подтвердил, что размер лунного изображения не изменился. Попробуйте в следующий раз, когда у вас возникнет соблазн выключить звук, и сэкономьте себе цену на марку.
Сесил Адамс
Отправить вопросы Сесил через Cecil @ straightdope.ком.
Похожие
Цитаты Horizon (102 цитаты)
«В долгом полете, после периодов кризиса и многих часов усталости, разум и тело могут разъединиться, пока порой они кажутся совершенно разными элементами, как если бы тело было лишь домом, с которым был связан разум, но никак не связаны. Сознание растет независимо от обычных чувств. Вы видите без помощи глаз, на расстояниях за визуальным горизонтом. Бывают моменты, когда существование кажется независимым даже от ума.Важность физического желания и непосредственного окружения погружена в понимание универсальных ценностей.В течение неизмеримых периодов я, кажется, отделился от своего тела, как если бы я был осознанием, распространяющимся сквозь пространство, над землей и на небеса, не стесненным временем или веществом, свободным от гравитации, которая связывает с тяжелыми человеческими проблемами мира , Мое тело не требует внимания. Это не голодно. Здесь не тепло и не холодно. Он смирился с тем, чтобы его не трогали. Почему я потрудился принести это сюда? Я мог бы лучше оставить его на Лонг-Айленде или Санкт-ПетербургеЛуи, в то время как невесомый элемент, который жил в нем, мелькает в небе и смотрит на планету. Это существенное сознание не нуждается в теле для своих путешествий. Ему не нужны ни самолет, ни двигатель, ни инструменты, а только освобождение от плоти, какие обстоятельства, через которые я прошел, делают возможным.
Тогда что я — субстанция тела, которую я вижу своими глазами и чувствую своими руками? Или я это осознание, это большее понимание, которое обитает в нем, но распространяется через вселенную снаружи; часть всего существования, бессильная, но не нуждающаяся во власти; погруженный в уединение, но в контакте со всем творением? Бывают моменты, когда они кажутся неразделимыми, а другие — когда они могут быть разорваны на части самой простой вспышкой света.
Когда моя рука находится на палке, мои ноги на руле и мои глаза на компасе, это сознание, как крылатый посланник, выходит, чтобы посетить волны внизу, испытывая тепло воды, скорость ветра, толщина промежуточных облаков. Он идет на север к ледниковому побережью Гренландии, за горизонтом до края рассвета, впереди Ирландии, Англии и континента Европы, через космос к луне и звездам, всегда возвращаясь, неохотно, к смертной обязанности видя, что конечности и мышцы следили за их рутиной, пока ее не было.»
—
Чарльз А. Линдберг,
Дух Святого Луи
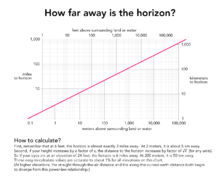 Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.
Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.