Нормы ГТО активно сдают жители Бердска
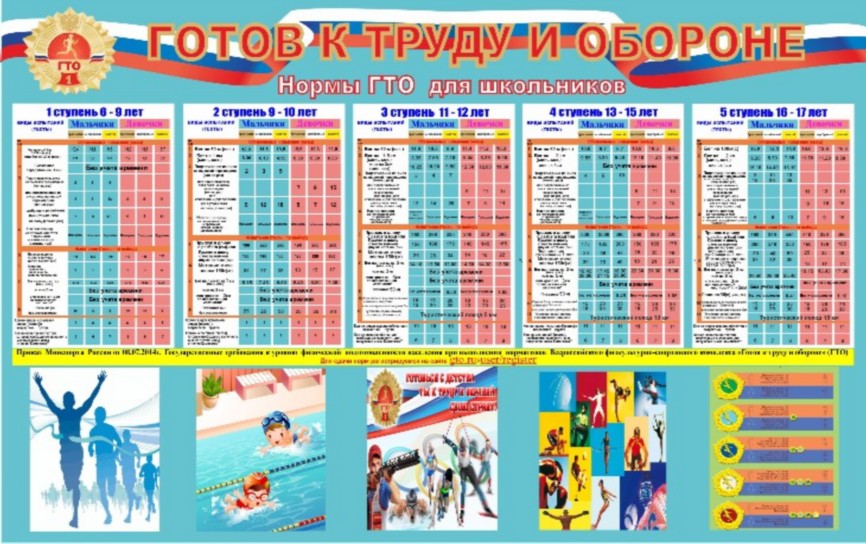
График приёма нормативов ГТО на май
Спорт
03.05.2023 16:52
Автор: Наталья Сковрунская, фото ОФКиС
Нормативы принимают на стадионе «Восток»
График приёма нормативов ГТО на май
Бердчане активно сдают нормативы ГТО. Получить знак ГТО могут все желающие.
Центр тестирования работает на базе спортивной школы «Авангарда», напомнил начальник отдела физкультуры и спорта Дмитрий Князев.
В частности, около 40 человек – воспитанники клуба боевых искусств – сдавали нормы ГТО в минувшую субботу. Кроме того мобильный цент тестирования «Авангард» может принять нормативы ГТО прямо в школе. В частности вчера, 2 мая, в школе №5 ГТО сдавали 96 учащихся. Как отметил руководитель центра тестирования ГТО Александр Посевков, данные дисциплины все ребята выполнили на знак отличия ГТО.
По понедельникам и четвергам нормативы ГТО можно сдать на стадионе «Восток». Приглашаются все желающие.
Центр тестирования ГТО «Готов к труду и обороне» базируется в муниципальном бюджетном учреждении дополнительного образования «Спортивной школе «Авангард» , находящейся по адресу: Новосибирская область, г.
Бердск, ул. Боровая д. 101/1. Телефон: 8 (38341) 4-41-95.
Население Бердска по последним данным превышает 102 тысячи человек, нормы ГТО можно сдавать до 79 лет — это крайняя ступень. Таким образом, по подсчетам руководителя отдела физкультуры и спорта, 80 тысяч бердчан по возрасту подходят для сдачи нормативов.
– Горожане сдают нормативы ГТО очень активно. Все спортсмены, занимающиеся у нас, сдали нормативы и имеют значки ГТО. В основном приходит молодёжь – знак ГТО даёт дополнительные баллы при поступлении в вуз. Сдают нормативы и пенсионеры и инвалиды, некоторые из них получают золотые знаки. Активно работаем со школами – разработан план, согласовывается время с учителями физической культуры, специалисты выходят в общеобразовательные учреждения и принимают нормативы прямо там, — говорит Дмитрий Сергеевич.
По итогам 2022 года среди 35 муниципальных образований Новосибирской области находится на 14 месте по количеству сдавших нормативы ГТО жителей.
График приема нормативов испытаний Всероссийского физкультурно-спортивного комплекса «Готов к труду и обороне» (ГТО) на май 2023 г.
| Дата/время | Вид испытания | Место проведения/ контакты |
| 11.05.2023/11.00-14.00ч. (четверг) | ОФП, подтягивание на низкой перекладине 90см, пресс за 1 мин., наклон вперед., прыжок в длину, отжимание, челночный бег 3х10 м. рывок гири 16 кг.), бега короткие длинные дистанции | Стадион «Восток», ул. Спортивная 5, т.8(38341)4-41-95 |
| 15.05.2023/11.00-14.00ч. (понедельник) | ОФП, подтягивание на низкой перекладине 90см, пресс за 1 мин., наклон вперед., прыжок в длину, отжимание, челночный бег 3х10 м. рывок гири 16 кг.), бега короткие длинные дистанции | Стадион «Восток», ул. Спортивная 5, т.8(38341)4-41-95 |
| 18.05.2023/11.00-14.00ч. (четверг) | ОФП, подтягивание на низкой перекладине 90см, пресс за 1 мин. , наклон вперед., прыжок в длину, отжимание, челночный бег 3х10 м. рывок гири 16 кг.), бега короткие длинные дистанции | Стадион «Восток», ул. Спортивная 5, т.8(38341)4-41-95 |
| 22.05.2023/11.00-14.00ч. (понедельник) | ОФП, подтягивание на низкой перекладине 90см, пресс за 1 мин., наклон вперед., прыжок в длину, отжимание, челночный бег 3х10 м. рывок гири 16 кг.), бега короткие длинные дистанции | Стадион «Восток», ул. Спортивная 5, т.8(38341)4-41-95 |
| 29.05.2023/12.00-14.00ч. (четверг) | ОФП, подтягивание на низкой перекладине 90см, пресс за 1 мин., наклон вперед., прыжок в длину, отжимание, челночный бег 3х10 м. рывок гири 16 кг.), бега короткие длинные дистанции | Стадион «Восток», ул. Спортивная 5, т.8(38341)4-41-95 |
| — | Внимание! Более полная информация находится на сайте https://dussh-avangard. nsk.sportsng.ru/ (возможны изменения в графике) | т.8(38341)4-41-95 |
Мы физкультуру выбираем, Сдадим все нормы ГТО! / Комплекс ГТО. Новости / Комплекс ГТО
Главная > Комплекс ГТО > Комплекс ГТО. Новости > Мы физкультуру выбираем, Сдадим все нормы ГТО!
В феврале в спортивном зале Электромашиностроительного колледжа стартовал традиционный Зимний фестиваль Всероссийского физкультурно-спортивного комплекса «Готов к труду и обороне». Мероприятия фестиваля организуют и проводят специалисты Центра тестирования – отдела ВФСК ГТО Спортивного центра «Физкультура и здоровье». Идея прежняя: повысить уровень физической активности граждан и вместе с тем улучшить здоровье нации.
Студенты и сотрудники Электромашиностроительного колледжа прошли тестирование по гимнастическим видам нормативов Комплекса ГТО в соответствии с IV-VIII возрастной ступенью комплекса (16-49 лет) в спортивном зале колледжа на ул.
Варшавская, д. 7. В программу первых соревнований в рамках зимнего фестиваля вошли такие испытания, как наклон туловища, сгибание и разгибание рук в упоре лежа, подтягивание из виса на высокой перекладине, поднимание туловища из положения лежа на спине, прыжок в длину с места и челночный бег.
Лучшие результаты в V возрастной ступени в челночном беге среди юношей у Артема Григорьева и Егора Воронина. В наклоне на скамье среди своих ровесников самыми гибкими оказались Егор Костин и Егор Дергачев, сумев наклониться на 18 см. В сгибании и разгибании рук в упоре лежа максимальный результат –63 раза продемонстрировал Василий Бурвенев, и 55 раз отжался от пола Даниил Лабуренко.
Максим Гурский стал лучшим в поднимании туловища из положения лежа –выполнив это упражнение 65 раз за минуту, и Дмитрий Абашкин в этом испытании выполнил упражнение – 58 раз за минуту. В прыжке в длину с места сильнейшим оказался Василий Бурвенев и Максим Гурский – они смогли прыгнуть на 260 см. Максим Гурский, также показал лучший результат в подтягивании из виса на высокой перекладине – 20 раз.
Среди преподавателей колледжа лучшие результаты продемонстрировали преподаватели физического воспитания. Результаты Виктора Спицина (XI ступень) составили 15 см ниже уровня скамьи в наклоне туловища, 30 раз в поднимании туловища из положения лежа на спине. Его коллега Анатолий Безуспарцев (VII ступень) продемонстрировал результат 17 см ниже уровня скамьи в наклоне туловища и 225 см в прыжках в длину с места.
Продолжат Зимний фестиваль ГТО студенты и преподаватели организаций средних и высших учебных заведений Московского района Санкт-Петербурга. Также в парке Авиаторов пройдут соревнования по скандинавской ходьбе среди представителей возрастных ступеней от 60 лет и старше. Бег на лыжах в свободном стиле будет проводиться для представителей всех возрастных ступеней. Все это также входит в программу Зимнего фестиваля ГТО. Зимними месяцами не заканчивается тестирование нормативов Всероссийского физкультурно-спортивного комплекса, весной и осенью можно также сдать нормативы или улучшить свои результаты.
За успешное выполнение нормативов комплекса ГТО вручается знак отличия бронзового, серебряного или золотого достоинств в каждой возрастной ступени и это является показателем активной жизненной позиции гражданина Российской Федерации, его стремление к здоровому образу жизни.
Векторные нормы: краткое руководство
Многие приложения, такие как поиск информации, персонализация, категоризация документов, обработка изображений и т. д., полагаются на вычисление сходства или различия между элементами. Два предмета считаются подобными, если расстояние между ними мало, и наоборот.
Как же рассчитать это расстояние? Что ж, каждый объект данных (элемент) можно рассматривать как n-мерный вектор, измерениями которого являются атрибуты (функции) данных. Таким образом, векторные представления позволяют вычислить расстояние между парами, используя стандартные меры сходства на основе векторов, такие как манхэттенское расстояние или евклидово расстояние, если назвать два.
При таких расчетах выходят нормы. Векторные нормы занимают важное место в контексте машинного обучения, поэтому в этой статье мы сначала постараемся понять основы нормы и ее свойств, а затем рассмотрим некоторые из наиболее распространенных векторных норм.
Общие векторные нормы в машинном обучении Парул ПандейСортировка фреймов данных в Pandas: практическое руководство
Что такое норма?
Норма — это способ измерения размера вектора, матрицы или тензора. Другими словами, нормы — это класс функций, которые позволяют нам количественно определить величину вектора. Например, норма вектора X нарисованного ниже – это мера его длины от начала координат.
Изображение создано автором.Тема норм часто возникает в контексте машинного обучения:
- При определении функций потерь, т. е. расстояния между фактическими и прогнозируемыми значениями
- Как метод регуляризации в машинном обучении, например, гребень и лассо методы регуляризации.
- Даже такие алгоритмы, как SVM, используют понятие нормы для вычисления расстояния между дискриминантом и каждым опорным вектором.
Как мы представляем нормы?
Норма любого вектора X обозначается двойной чертой вокруг него и записывается следующим образом:
Изображение создано автором.
Каковы свойства нормы?
Рассмотрим два вектора X и Y, имеющих одинаковый размер и скаляр- ?. Функция считается нормой тогда и только тогда, когда она удовлетворяет следующим свойствам:
Каковы свойства нормы?
- Неотрицательность: всегда должна быть неотрицательна.
- Определенность: Он равен нулю тогда и только тогда, когда вектор равен нулю, т. е. нулевой вектор.
- Неравенство треугольника: норма суммы двух векторов не больше суммы их норм.
- Однородность: при умножении вектора на скаляр норма вектора умножается на абсолютное значение скаляра.
Давайте посмотрим, как эти качества представлены математически.
Неотрицательность
Изображение создано автором.
Определенность
Изображение создано автором.
Неравенство треугольников
Изображение создано автором.
Однородность
Изображение создано автором.Любая функция действительного значения вектора, удовлетворяющая четырем указанным выше свойствам, называется нормой.
Какие существуют стандартные нормы?
Можно определить множество функций, удовлетворяющих описанным выше свойствам. Рассмотрим двумерный вектор-столбец X следующим образом:
Изображение, созданное автором.Теперь мы можем рассчитать некоторые стандартные нормы для X, начиная с нормы L¹.
Что такое L¹ норма / манхэттенская норма?
Норма L¹ определяется как сумма абсолютных значений компонентов данного вектора. Поскольку у нас есть вектор X только с двумя компонентами, L¹ норма x может быть записана как:
Изображение, созданное автором.
Обратите внимание на представление с единицей, написанной в качестве нижнего индекса. Эта норма также называется нормой Манхэттена или нормой такси, вдохновленной районом Манхэттена в Нью-Йорке. Норма L¹ обычно представляет собой расстояние, которое такси должно будет проехать от пункта отправления до пункта 9.0097 х .
Математическая запись
Норма L¹ может быть математически записана как:
Изображение создано автором.Каковы свойства нормы L1/Манхэттен?
- Норма L¹ используется в ситуациях, когда полезно различать нулевые и ненулевые значения.
- Норма L¹ увеличивается линейно вокруг начала координат.
- Он используется в регрессии Лассо (оператор наименьшего абсолютного сокращения и выбора), которая включает добавление L¹ нормы коэффициента в качестве штрафного члена к функции потерь.
Что такое норма L²/евклидова норма?
L² — это наиболее часто используемая норма и наиболее часто встречающаяся в реальной жизни норма.
Норма L² измеряет кратчайшее расстояние от начала координат. Он определяется как корень суммы квадратов компонентов вектора. Итак, для нашего заданного вектора X норма L² будет:
Норма L² настолько распространена, что иногда ее также обозначают без индекса:
Изображение создано автором.Норма L² также известна как евклидова норма в честь знаменитого греческого математика, которого часто называют основателем геометрии. Евклидова норма по существу означает, что мы имеем в виду евклидово расстояние.
Математическое обозначение
Норма L² может быть математически записана как:
Изображение создано автором.Каковы свойства нормы L2?
- Норма L² наиболее часто используется в машинном обучении
- Поскольку он влечет за собой возведение в квадрат каждого компонента вектора, он не устойчив к выбросам.
- Норма L² медленно увеличивается вблизи начала координат, например, 0,¹² = 0,01
- Используется в гребневой регрессии, которая включает добавление коэффициента нормы L² в качестве штрафного члена к функции потерь.
Какова норма L∞/Max?
Норма L∞ определяется как абсолютное значение наибольшего компонента вектора. Поэтому ее также называют максимальной нормой. Итак, продолжая наш пример с двумерным вектором X, имеющим две компоненты, то есть x₁ и x₂, где x₂ > x₁, нормой ∞ будет просто абсолютное значение x₂.
Изображение создано автором.
Математическая запись
Норма L∞ может быть математически записана как:
Изображение создано автором.Каковы свойства максимальной нормы?
- Норма L∞ упрощается до абсолютного значения наибольшего элемента вектора.
Что такое Lᵖ норма?
Теперь мы можем обобщить идею того, что известно как p-норма. В некотором смысле мы можем вывести все остальные нормы из p-нормы, варьируя значения p. То есть, если вы замените значение p единицей, двумя и ∞ соответственно в приведенной ниже формуле, вы получите нормы L¹, L² и L∞.
Математическая запись
Норма Lᵖ может быть математически записана как:
Изображение создано автором.
Здесь важно помнить, что каждая из приведенных выше норм соответствует свойствам норм, упомянутых в начале.
Что происходит, когда p равно нулю?
Когда это происходит, мы можем назвать значение L⁰ «нормой». Однако технически это не является нормой, поскольку нарушает однородность норм, как ясно показывает этот отрывок Википедии . Чтобы прояснить ситуацию, мы можем сказать, что «норма» L⁰ полезна, когда мы хотим знать количество ненулевых компонентов в векторе. Это означает, что разреженность можно моделировать с помощью «нормы» L⁰.
Изображение создано автором.Разреженность — важная концепция машинного обучения, поскольку она помогает повысить надежность и предотвратить переобучение.
Подробнее о науке о данныхКак решить FizzBuzz
Суммирование векторных норм
В этой статье рассматривается понятие векторной нормы, ее свойства и некоторые часто используемые нормы, с которыми мы сталкиваемся в машинном обучении. Однако мы не можем закончить эту статью, не реализовав различные нормы с помощью Python и не поняв их геометрическую интерпретацию.
Это помогло бы нам понять, почему во многих учебниках норма L¹ представлена в виде ромба, а норма L² — в виде круга.
Вам также могут пригодиться эти ресурсы по линейной алгебре.
линейная алгебра — Понимание теоремы о том, что все нормы эквивалентны в конечномерных векторных пространствах
Вот один подход, упомянутый в книге анализа Ланга.
Пусть $V$ — $\mathbb{R}$-векторное пространство с базисом $e_1 ,\ldots,e_k$.
$ \| x_1 e_1 + \ldots + x_k e_k \|_\infty := \max\{ |x_1|, \ldots, |x_k| \} $ — норма на $ V $.
$ \| \ldots \|_{\infty} $ делает $ V $ полным.
Пусть $(v_j)_{j \geq 1} = (v_1, v_2, \ldots )$ — последовательность Коши в $V$. Выражая относительно базисных векторов, $$ (v_1, v_2, \ldots) = (e_1, e_2, \ldots, e_k) \begin{pmatrix} v_{11} &v_{12} &\ldots \\ v_{21} &v_{ 22} &\ldots \\ \vdots &\vdots &\ddots \\ v_{k1} &v_{k2} &\ldots \end{pmatrix}, \, \text{каждый }v_{ij} \in \mathbb{ R} .
$$ То есть $v_{ij}$ есть $e_i$-координата $v_j$.
Обратите внимание на последовательность $ (v_{1j})_{j \geq 1} = (v_{11}, v_{12}, v_{13}, \ldots ) $ по Коши [ , потому что $ | v_{1n} — v_{1m} | \leq\| v_n — v_m \|_{\infty} $ ]. Точно так же последовательности $ (v_{1j}), (v_{2j}) , \ldots, (v_{kj}) $ являются Коши, следовательно, сходящимися.
Итак, пусть $ v_{1j} \to c_1, \ldots, v_{kj} \to c_k $ as $j \to \infty $. Теперь $ v_j \to c_1 e_1 +\ldots + c_k e_k $ as $ j \to \infty $ [ , потому что $\| v_j — (c_1 e_1 + \ldots + c_k e_k) \|_\infty $ $ =\max \{ |v_{1j} — c_1| , \ldots, |v_{kj} — c_k | \} $ $ \to 0 $ as $ j \to \infty $], по мере необходимости.
Теперь пусть $ \| \ldots\| $ — любая норма на $V$. Попробуем показать $ \| \ldots\| $ и $ \| \ldots \|_{\infty}$ эквивалентны на $V$ по индукции по размерности $k$ нормированного пространства. Итак, давайте предположим, что $ \| \ldots\| $ и $ \| \ldots \|_{\infty} $ эквивалентны на каждом собственном подпространстве в $ V $.
{-1} \| в_н \| $ $\big($и, следовательно, $ \| w_n \| < \frac{1}{n} \big) $. Также каждый $w_n$ имеет $1$ в качестве координаты.Выражение последовательности $ (w_n)_{n \geq 1} $ относительно базисных векторов, $$ (w_1, w_2, \ldots ) = (e_1, e_2, \ldots, e_k) \begin{pmatrix} w_{11} &w_{12} &\ldots \\ w_{21} &w_{22} &\ldots \\ \vdots &\vdots &\ddots \\ w_{k1} &w_{k2} &\ldots \end{pmatrix}. $$ Каждый столбец имеет $ 1 $, и каждая запись имеет величину $ \leq 1 $.
Итак, существует $ T \in \{ 1, 2, \ldots, k \} $ такое, что в строке $ w_{T 1}, w_{T 2}, \ldots $ бесконечно много $ 1 $s. Пусть $ J := \{ j : w_{T j} = 1 \} $ будет позициями, в которых $1$ встречаются в этой строке.
Теперь сосредоточимся на последовательности $ (w_j — e_T)_{j \in J} $.
Во-первых, поскольку $ (w_n)_{n \geq 1} $ сам по себе сходится к $ 0 $ относительно $ \| \ldots\| $ эта последовательность $ (w_j — e_T)_{j \in J} $ сходится к $ (-e_T) $ w.r.t $ \| \ldots\| $.
Обратите внимание, что последовательность $(w_j — e_T)_{j \in J} $ лежит в подпространстве $V_T := \{ x_1 e_1 + \ldots + x_k e_k : x_T = 0 \} $.
{-1} \| в_н \| $ $\big($и, следовательно, $ \| w_n \| < \frac{1}{n} \big) $. Также каждый $w_n$ имеет $1$ в качестве координаты.